État de la recherche
L’étude des anciens systèmes de pesée a une longue tradition remontant au XIXe s. au cours duquel ont été produites des synthèses reposant sur le croisement des données entre l’identification d’unités métrologiques dans les sources textuelles antiques, l’épigraphie et les apports de la numismatique1. Ces travaux ont permis de reconstituer une grande partie des systèmes métrologiques utilisés durant l’Antiquité en Méditerranée centrale et orientale.
Cet intérêt pour les systèmes de mesure et la manière dont les populations anciennes mesuraient le monde qui les entourait a perduré jusqu’à nos jours de manière parfois hétérogène, en suivant différentes écoles de pensées et orientations méthodologiques en fonction du temps et des lieux. Le caractère multiscalaire, multipolaire et multidirectionnel de ces entreprises les rend difficile à tracer. Mis à part dans le champ de la numismatique, dont les apports au domaine sont cruciaux mais dont un état de l’art nécessiterait une thèse à elle seule, rares sont les travaux qui ont réellement fait école. Nous tenterons ici de présenter les jalons historiographiques principaux qui ont conditionné les méthodes d’approche des processus de mesure pondérale de l’Europe des âges des Métaux.
I. La Méditerranée centrale et orientale :
creuset de la métrologie historique
Le terme de “métrologie historique” est défini par Witold Kula, un historien de l’économie d’origine polonaise, dès 1963 dans son Problemy i metody gospodarczej. Cet ouvrage est traduit dans plusieurs langue et largement diffusé dans les années qui suivent participant ainsi à la diffusion du terme et à sa réutilisation postérieure2. Il définit la métrologie historique comme une science auxiliaire de l’histoire, et de l’histoire économique en particulier, qui porte sur la connaissance des mesures et systèmes de mesure utilisés dans le passé3. Cependant, si l’expression et le sens qu’elle renferme apparaissent avec W. Kula, l’origine de la démarche d’étude des systèmes de mesures anciens prend ses racines plusieurs décennies plus tôt et avec pour terrain d’étude privilégié la Méditerranée orientale et centrale.
Il est en effet impossible d’aborder la métrologie historique sans parler du Bassin Méditerranéen et plus particulièrement des populations qui y fleurissent durant tout l’âge du Bronze. La construction et l’évolution de la métrologie historique tout comme son application en Europe occidentale sont en effet intrinsèquement liés aux travaux réalisés durant plus d’un siècle sur la Méditerranée centrale et orientale.
1. Une historiographie de la métrologie en Méditerranée
L’intérêt pour les systèmes de mesure pondérale anciens se perçoit dans la production littéraire des Antiquaires dès la première moitié du XIXe s. Le philosophe et Antiquaire allemand August Böckh (ou Boeckh), connu pour sa contribution à l’économie politique athénienne4, en est alors l’un des précurseurs par son imposante synthèse analytique sur l’ensemble des métrologies pondérales anciennes publiée en 18385. Son travail, pionnier dans le genre, s’appuie sur une grande variété de sources (mentions dans des textes antiques, dans les poèmes homériques ou l’Ancien Testament, textes de réformes économiques, numismatique…) pour restituer les systèmes métrologiques des grandes civilisations connues en Méditerranée centrale et orientale depuis l’âge du Bronze jusqu’à l’Antiquité. L’auteur y développe l’idée que les systèmes pondéraux anciens reposent sur une construction volontairement scientifique, dérivées de mesures de capacités, elles-mêmes obtenues des mesures linéaires, et dont le berceau serait la Mésopotamie6.
Méthodologiquement, le travail de d’A. Böckh repose sur l’idée que tous les systèmes pondéraux sont interconnectés et résultent du même principe visant à la mesure de la masse d’objets et de marchandises et peuvent donc être étudiés à partir de cette composante. La “métrologie comparative” (vergleichende Metrologie) qu’il met en place vise à comprendre les systèmes métrologiques anciens par l’approche comparative des différentes unités connues pour des périodes plus récentes, notamment celles de l’Antiquité Classique7.
La “métrologie comparative”, poursuivie notamment par Friedrich Otto Hultsch8 et Carl Friedrich Lehmann-Haupt9 dans la deuxième moitié du XIXe s., va rapidement s’orienter vers la recherche de relations entre unités et la restitution de routes de diffusion des systèmes métrologiques, d’est en ouest, depuis l’apparition des premières séries mésopotamiennes jusqu’à la période gréco-romaine. Les possibilités de d’oscillation métrologique des unités sont généralement ignorées ce qui entraine la définition de nombreuses variantes de mêmes unités comprises comme des choix volontaires.
Cette vision de la métrologie sera critiquée dès le XIXe s., notamment par William Ridgeway qui s’intéresse aux origines des systèmes de pesée et de monnaie métallique en Grèce10 et qui voit dans l’origine du système de valeur grec la tête de bétail et dans les premières unités pondérales des pesées de graines destinées à mesurer l’or avec précision.
Il faut toutefois attendre les travaux d’Oskar Viedebantt11 pour voir émerger une nouvelle théorisation de l’étude métrologique, la “métrologie inductive”, et surtout la création du principe de Normzone. Ce terme renvoie à l’intervalle de variabilité à l’intérieur duquel un standard métrologique ancien est considéré comme juste. Cet intervalle possède une valeur minimale, une valeur maximale et un point de concentration et de densification de l’unité. Ce concept va bien évidemment à l’encontre de l’idée développée par A. Böckh et ses successeurs voulant que les standards pondéraux soient parfaitement justes et que les variations observées correspondent à des évolutions ou à des adaptations.
Les recherches d’O. Viedebantt sont relativement mal reçues en raison de son opposition farouche à l’école traditionnelle, de la complexité qu’amènent ces idées dans la recherche d’unités pondérales mais également du caractère spéculatif de ses démonstrations. Toutefois, le concept de Normzone apparait parfois de manière plus ou moins implicite comme dans les recherches empiriques menées par l’égyptologue anglais William Matthew Flinders Petrie12 ainsi que dans celles de plusieurs chercheurs spécialistes du Proche-Orient13.
Cette phase d’élaboration théorique laisse petit à petit la place à l’émergence de nouveaux courants et écoles de recherche, qui vont fixer aux problématiques de métrologie et de numismatique le cadre historique qui lui fait souvent défaut jusque-là. Cette nouvelle dynamique constitue l’émergence de la “métrologie historique” telle qu’elle est définie par W. Kula14 dans le contexte de la recherche métrologique au Proche-Orient et est en grande partie menée par un groupe de chercheurs italiens, historiens et assyriologues de formation. Parmi ces travaux, publiés entre la fin des années soixante et la fin des années quatre-vingt-dix, il faut notamment citer les recherches fondamentales de Nicola Parise au Proche-Orient15 qui est rapidement rejoint par Carlo Zaccagnini16 puis ponctuellement par Mario Liverani17. Leurs travaux se fondent sur un cadre de références historiques, sociales et économiques solides qui sert de base à leurs interprétations. Ces différents travaux permettent principalement d’admettre l’existence d’unités majeures largement diffusées en Méditerranée orientale : la mine et le talent. Les travaux de l’école métrologique italienne, notamment ceux de N. Parise, permettent de préciser le rapport entretenu par la mine de 470 g, employée dans une grande partie de la Méditerranée orientale et les différentes subdivisions qui lui sont connues18.
Toutefois, la donnée archéologique reste relativement anecdotique dans ces recherches. Bien que certains auteurs aient publié des instruments de pesée bien avant eux19, les premiers à centrer réellement un discours sur les poids de balance viennent d’outre-Atlantique. Ce sont Karl Petruso et Cemal Pulak qui vont, dans le cadre de leurs thèses respectives, proposer de nouvelles méthodes d’analyse de ces artefacts et leur donner ainsi une place centrale dans le débat sur la métrologie ancienne. Les travaux de K. Petruso sur le sujet commencent dans les années 1970 et 1980, mais c’est en 1992, qu’il publie l’étude de la série de poids de balance découverts à Ayia Irini (Kéos, Cyclades, Grèce)20, la partie la plus importante de sa thèse de doctorat soutenue en 197821. La thèse de C. Pulak porte quant à elle sur les ensembles de poids de balances des épaves d’Uluburun (fin du XIVe s. a.C.) et du Cap Gelidonya (fin du XIIIe-début du XIIe s. a.C.)22 dont il publie des articles synthétiques quelques années plus tard.
Les deux études sont très proches d’un point de vue méthodologique. Elles accordent une grande place à l’artefact archéologique : critères d’identification, classement typologique, caractéristiques mécaniques et technologiques, stabilité des matériaux, etc. Les auteurs s’interrogent également tous deux sur les facteurs influant sur l’identification d’un standard pondéral et optent pour une approche statistique de la donnée archéologique amenant aux premières utilisations de l’analyse quantale sur des poids de balance23.
Depuis la fin des années 1990 et le début des années 2000, la dynamique de recherche en métrologie ne s’est pas enrayée. La Méditerranée et “l’école italienne” continuent à jouer un rôle de premier plan. Les thématiques ont toutefois dépassé la simple recherche d’unités métrologiques et s’orientent vers la caractérisation des interconnections entre différentes sphères économiques d’échelle régionale et différents systèmes de pesée24. La place de la donnée archéologique dans ces problématiques est désormais évidente. L’une des aspirations de ce courant de recherche est le développement d’une “métrologie globale” profitant des apports de la “métrologie historique” et ceux de la “métrologie archéologique” pour une prise en compte des données textuelles, de la contextualisation historique des systèmes de pesée et l’application des méthodes des sciences archéologiques aux poids de balance, aux lingots et aux matières premières25. La métrologie pondérale est alors appréhendée non plus comme un simple concept théorique intemporel mais comme une pratique quotidienne qui évolue en fonction de critères matériels, sociaux et économiques.
2. La comparaison métrologique
Panorama des systèmes pondéraux
La comparaison métrologique tient une grande place dans le discours global sur les poids et balance. Pour comprendre le développement des études sur la métrologie pondérale en Europe, il est donc primordial de présenter tout d’abord l’histoire des poids et mesures de la Méditerranée centrale et orientale qui reviennent systématiquement comme un ancrage de référence dans les études sur le sujet. L’objectif ici est de dresser un panorama des unités et systèmes pondéraux principaux qui peuvent servir à l’approche comparative en se fondant sur certains des travaux les plus récents sur le sujet.
Il n’est pas aisé de déterminer exactement à quel endroit, dans le monde, ont été développés les premiers instruments de pesée. Il semble cependant qu’actuellement, les plus anciens vestiges archéologiques liés à la création d’une métrologie pondérale, construite sur des masses standardisées, soient attribuables à l’Égypte prédynastique, au début du IVe millénaire a.C. Cette époque correspond à une période de complexification et de hiérarchisation sociale qui se reflètent notamment dans le traitement funéraire des défunts26. Les poids de balance en question sont de forme variée, façonnés en calcaire, et ont été mis au jour à Naqada, en Haute Égypte. Ils sont basés sur une unité d’environ 12-13 g, connue postérieurement sous le nom de beqa ou deben d’or, cette unité étant principalement utilisée pour la mesure de ce métal. Ce système aura une postérité plus longue que n’importe quel autre puisqu’il était toujours en vigueur au début du IIIe s. a.C. et toujours associé alors à la pesée de métaux précieux27.
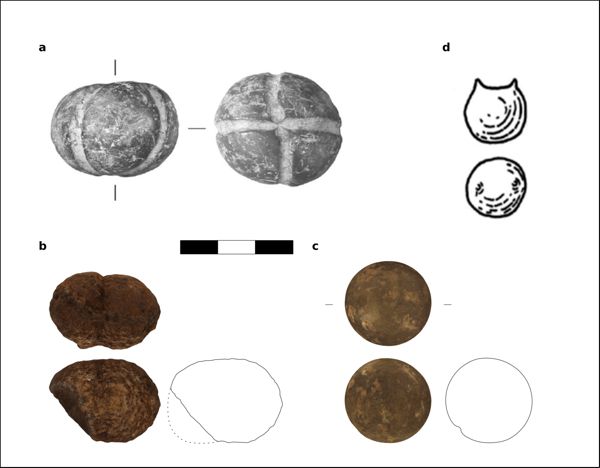
Ce développement précoce se voit, par la suite, codifié et complexifié au sein du monde égyptien en même temps que des systèmes comparables apparaissent aux alentours. Six poids retrouvés à Uronarti (Nubie), une île à proximité de la deuxième cataracte du Nil, montrent la perduration du beqa. Les objets, datés de 1850 a.C. sont tous marqués du hiéroglyphe désignant l’or associé à des marques numériques : un trait étant égal à un beqa. Ce lot de poids nous renseigne donc sur l’utilisation, à cette époque au moins, de multiples équivalant à 5 beqa (61-66,3 g), 6 beqa (74,5 g), 7 beqa (92,0 g) et 9 beqa (116 g ; fig. 1-1)28.

Les textes du Nouvel Empire (1550-1077 a.C.) nous renseignent sur la standardisation de nouvelles unités et leurs correspondances arithmétiques. Ainsi, un deben est égal à dix qedets et dix debens à un sep. Le qedet est alors égal à environ 9,33 g et correspond à une unité destinée au pesage du grain29. Ces masses ne sont pas fixes et précises, et peuvent varier en fonction du temps et de l’espace comme le montre une étude basée sur 412 poids de balance entreposés au Musée du Caire et qui attribue au qedet une valeur comprise entre 9 et 9,5 g. Les inscriptions apposées sur les instruments attestent de l’existence d’artisans dévolus à la fabrication des poids dans chaque cité30. En raison de la multiplication des spécialistes fabricant ces objets et de la durée de vie particulièrement longue des unités pondérales égyptiennes (environ trois millénaires dans le cas du beqa), il est complètement compréhensible que celles-ci subissent des variations.
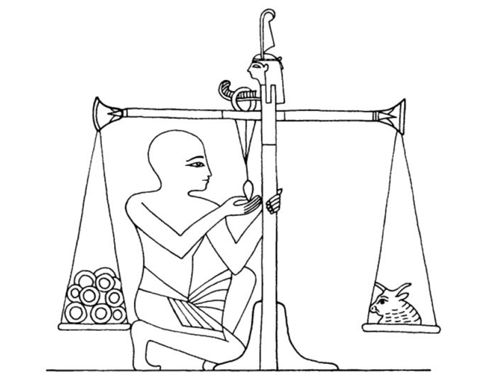
Les peintures murales des tombes ou des temples représentent des scènes de pesées où semblent être utilisés des poids zoomorphes. Sur le détail d’une peinture murale de la tombe 181 (fig. 1-2), on peut notamment voir un individu contrôlant l’équilibre d’une balance (au moyen d’un fil à plomb), qui accueille des anneaux en or sur son plateau gauche contrebalancés par un poids en forme de tête de bœuf sur son plateau droit31. Deux poids en granit en forme de tête bovine sont connus, pesant 4 et 20 kg. Ces objets, peut-être destinés à la pesée de très grandes quantités d’or, sont rares et une étude menée sur les poids conservés au musée du Caire montre une concentration des poids pour les fractions de 1/5, 1/3 et 1/2 qedet et pour ses multiples 2, 3, 5, 10 et 20, soit approximativement entre 1,8 et 180 g32.
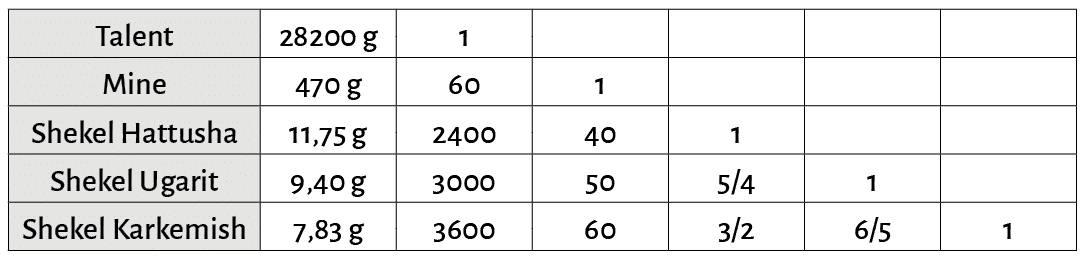
L’un des travaux récents les plus complets sur les systèmes métrologiques du Proche-Orient est l’ouvrage de Enrico Ascalone et Luca Peyronel33 qui s’attèle à l’inventaire des poids de balance trouvés sur le site d’Ebla ainsi que la remise en contexte des systèmes pondéraux et des instruments de pesée du Proche-Orient depuis leur apparition vers la fin du IVe millénaire a.C. jusqu’à la fin du Bronze moyen (v. 3200-1600 a.C.). Les systèmes métrologiques de Méditerranée orientale sont caractérisés par l’utilisation d’unités principales (les mines) servant de base à la création d’unités plus légères (les shekels) et plus lourdes (les talents). Une première mine est bien attestée par l’épigraphie de la fin de l’âge du Bronze, mais aussi par les études systématiques qui ont été effectuées sur le matériel de pesée34 : d’une valeur approximative de 470 g, elle est divisée, en fonction des lieux, en 60 shekels de 7,83 g, 50 shekels de 9,40 g et 40 shekels de 11,75 g35 (fig. 1-3).
La portée et la postérité de ces différentes unités n’est pas la même mais il semble que la majorité se maintienne plus ou moins jusqu’au changement d’ère. Ainsi le shekel de 9,4 g est bien identifié en Méditerranée orientale et dans l’Égée36 ; une unité d’une valeur similaire semble toujours active durant la période Hellénistique37. Il faut rajouter à cela un shekel d’environ 5-5,9 g, identifié en particulier à Troie et Tarse et à la diffusion géographique et chronologique complexe38.
Une autre mine, à l’ample diffusion géographique, est essentiellement dédiée à la pesée de la laine. Sa masse est comprise entre 650 et 680 g, elle est divisible en 100 shekels de 6,5-6,8 g, ce qui correspond à une division par 70 de la mine de 470 g39. L’unité d’environ 61-62 g (Normzone de 8 %) identifiée par K. Petruso autour de la Mer Égée pour la fin de l’âge du Bronze40 correspond vraisemblablement à une adaptation du dixième de cette mine.
Des mines “hybrides” sont également attestées et résultent de l’application de différents systèmes de comptage à certaines unités. Ainsi, une mine de 564 g correspondrait à l’utilisation du shekel de 9,4 g avec un système sexagésimal (9,4 x 60 = 564)41. De manière similaire, l’emploi d’un système décimal pour multiplier la “darique” de 8,4 g aurait pour conséquence la création d’une mine hybride de 420 g (8,4 x 50 = 420)42.
Bien qu’il ne rentre pas directement dans les normes métrologiques officielles en vigueur – autrement dit celles mentionnés dans les sources écrites – il semblerait que la pratique courante de la pesée ait amené au développement d’une unité usuelle d’environ 47 g. Bien qu’absente des données textuelles, celle-ci est attestée par la forte concentration de poids de balance autour de cette valeur ainsi que par l’utilisation de ses multiples, vraisemblablement dès le début du IIIe millénaire a.C. et sur une zone large englobant le Levant, l’Anatolie et la partie interne de l’actuel territoire syro-palestinien43. Son usage pourrait être la réponse à un besoin de facilitation des conversions entre systèmes44 (fig. 1-4).

Le système pondéral utilisé en Mésopotamie dès le début du IIIe millénaire a.C. se distingue quelques peu des autres par l’utilisation d’un plus grand nombre de subdivisions et une existence particulièrement longue (vraisemblablement jusqu’à l’époque d’Alexandre le grand) malgré des variations assez élevées du standard. Cependant, E. Ascalone et L. Peyronel, sur la base de la documentation archéologique, lui attribuent les valeurs suivantes : une mine de 490-515 g (avec une moyenne d’environ 500 g) et un shekel de 8,2-8,5 g (moyenne d’environ 8,35 g)45.
Si les systèmes métrologiques mis en place durant le IIIe millénaire a.C. semblent persister en Méditerranée orientale et au Proche-Orient durant les siècles suivants, il est plus difficile de comprendre leur évolution dans l’Égée. Après le déclin de la culture de l’EBA II, aux alentours de 2250 a.C., les artefacts liés à la pesée se font plus rares. En Crête, seuls quelques poids ont été mis au jour pour la période des “Premiers Palais” (v. 2000-1700 a.C.)46.
La période des “Nouveaux Palais” en Crête (v. 1700-1400 a.C.) est en revanche plus propice à l’étude de la métrologie pondérale avec des poids se présentant comme des disques de plomb découverts sur plusieurs sites de Crête et des Cyclades. L’étude que réalise K. Petruso sur ces objets démontre l’utilisation d’un système basé sur une nouvelle unité “minoenne” d’environ 61 g (entre 60 et 65 g) et d’un système de comptage duodécimal basé sur les multiples 2 : 4 : 6 : 8 : 12 : 16 : 24 et des fractions 1/4 : 1/3 : 1/2 : 2/347.
La période des Palais Mycéniens (XIVe-XIIIe s. a.C.) offre un corpus plus limité. Les poids discoïdaux ne représentent pas le type privilégié sur le continent et les quelques dizaines d’artefacts publiés sont de formes variées (fusiformes, quadrangulaire, discoïdaux…). Si certains de ces objets peuvent correspondre au système minoen mis en place durant la période précédente, d’autres renvoient clairement à un ou plusieurs systèmes métrologiques différents. À ce jour, la métrologie pondérale mycénienne n’est pas clairement comprise faute d’une documentation étoffée et d’études spécialisées. On notera un fait étonnant : la présence de poids en pierre en forme de bobine, comme ceux datés du IIIe millénaire a.C., déposés dans des tombes mycéniennes ou abandonnés dans des niveaux d’occupation (fig. 1-5). Il est difficile de dire si ces objets ont gardé pendant près d’un millénaire leur vocation métrologique ou s’il s’agit d’une réutilisation plus ou moins opportuniste, métrologique ou non, d’un artefact ancien par les Mycéniens48.

(d’après Demakopoulou et al. 2010, fig. 67).
Les travaux de C. Pulak sur les lots de poids de balance de l’épave d’Uluburun confirment le maintien des shekels de 7,4 g, 8,3 g et 9,4 g ainsi que l’utilisation d’une probable unité de 10,5 g à la fin du XIVe s. a.C.49. Ceux de Cap Gelidonya en revanche, datés de la fin du XIIIe ou début du XIIe s. a.C., semblent montrer que si le shekel de 9,4 g est toujours utilisé, une unité de 7,1-7,3 g fait son apparition alors que les constructions métrologiques des lots montrent une adaptation probable à l’unité de 60-65 g identifiée par K. Petruso dans l’Égée.
La période correspondant en Europe occidentale au Bronze final, et donc au début de la période couverte par ce travail, n’est pas la mieux connue pour ce qui concerne la métrologie de la Méditerranée centrale et orientale. Entre le XIe et le VIIIe, les Chypriotes et les Phéniciens semblent jouer un rôle important dans la diffusion vers l’occident d’une unité de 5,8 g (correspondant à la moitié du shekel “hittite” de 11,75 g) et d’un shekel “phénicien” de 7,76 g (qui correspondrait à une version allégée du shekel “syrien” de 7,83 g) attesté par au moins trois lingots50. Les poids et lingots trouvés en Sardaigne dans les sites nuraghes, datés des VIIIe-VIIe s. a.C., renvoient ainsi à l’utilisation du shekel “hittite”, de sa moitié et potentiellement au dixième de l’unité égéenne de 65 g51. Plus tard, entre les VIIIe et IVe s., dans la région de Tyr, une unité de 8,02-8,42 g, qui correspond vraisemblablement au shekel mésopotamien de 8,3-8,4 g, est utilisée ainsi qu’une unité de 10,23-10,69 g qui se rapproche de celle identifiée dans l’épave d’Uluburun. À Sidon en revanche, les poids renvoient à un système construit autour d’une unité de 11,26-12,74 g pouvant correspondre soit à un shekel “hittite” de 11,75 g, soit à un shekel “hébreu” de 11,33 g52.
La tombe de Lefkandi (Eubée), datée aux alentours de 875-850 a.C., a livré 16 poids en pierre dont la construction pondérale renvoie à trois des standards utilisés à Tyr au VIIIe s. p.C. : ceux de 8,3 g, 10,5 g et 11,7 g53. Deux siècles plus tard, sur la même île, à Pithécusses, il semblerait qu’un standard égal à un statère d’argent soit utilisé et il est attesté par un poids de 8,79 g, correspondant à la moitié du statère. Ce dernier est découvert dans un espace interprété comme une forge54.
Il semble que le système du talent et de la mine d’Eubée, dérivé de standards employés originellement en Méditerranée orientale, se diffuse dans toute la Grèce pour peser l’argent, l’or et d’autres matériaux précieux de manière contemporaine à l’adaptation de l’alphabet phénicien par les Grecs. La mine d’argent en question est estimée à 432-436 g, mais comme la mine de 470 g plusieurs siècles avant, celle-ci est divisée différemment en fonction des lieux amenant à une multiplication des systèmes métrologiques55.
Par conséquent, la période archaïque grecque voit l’utilisation de nombreux systèmes métrologiques distincts dans un ensemble qu’Andrew Meadows et Kirsty Shipton jugent chaotique56. Ces différentes pratiques, qui dérivent en partie d’héritages mycéniens et de traditions du Levant et de la Mésopotamie57, amènent à l’emploi de 14 standards pondéraux distincts dans la frappe des pièces de monnaies d’argent entre le milieu du VIe et le début du Ve s. a.C.58. Les premières monnaies frappées en Ionie sont décrites comme des fractions d’un statère dont la masse diffère en fonction des communautés ou groupes de communautés. Ainsi, le statère milésien ou lydien pèse 14,1 g alors que celui d’Eubée s’élève à 17,5 g et que celui de Phokaïa s’inscrit entre les deux en accusant une masse de 16,5 g59. Les frappes monétaires s’alignent ainsi sur des systèmes pondéraux locaux sans volonté d’un alignement sur un standard macro-géographique qui faciliterait les échanges hors des frontières de chaque cité-état. La raison à cela est que la pièce de monnaie n’est vraisemblablement considérée en fonction de sa valeur faciale qu’à l’intérieur des frontières, où elle peut toujours être acceptée pour sa valeur faciale (en particulier pour payer les taxes)60, alors qu’à l’extérieur c’est la quantité de métal qu’elle renfermer qui est prise en compte, ce qui n’empêche alors pas de la thésauriser comme une quantité de matière précieuse, comme le montrent plusieurs dépôts concentrant des monnaies d’origines diverses61.
En ce qui concerne les systèmes métrologiques, ils sont connus pour la période archaïque essentiellement par des textes et quelques poids de balance. Ces derniers sont systématiquement exprimés en fractions du statère alors que l’argent (métal ou pièces de monnaies) est calculé en mines, soit deux systèmes métrologiques distincts qui permettent tous deux de mesurer des masses et dont il est possible de restituer les correspondances entre la fin du VIe s. et la fin du Ve s. a.C. (fig. 1-6)62.
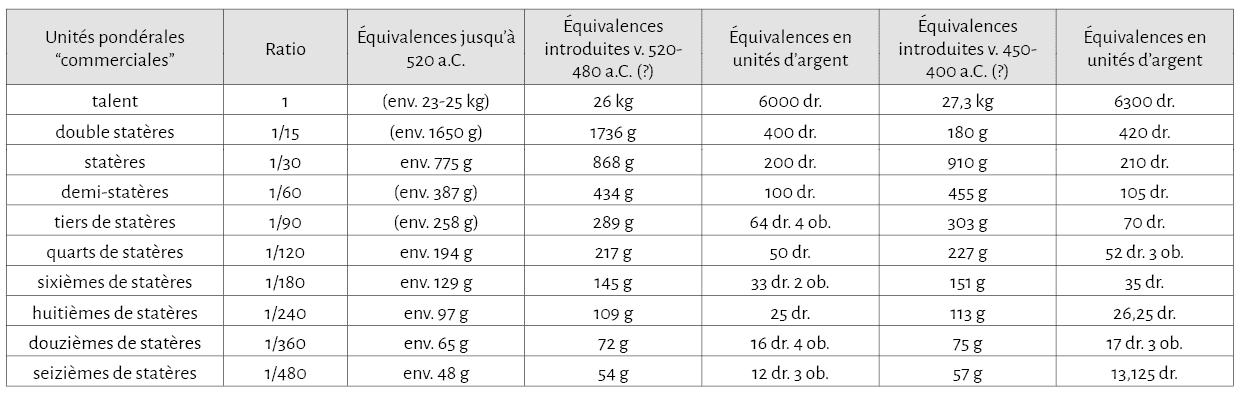
Les valeurs entre parenthèses ne sont pas attestées archéologiquement ; dr. = drachmes ; ob. = oboles.
Du point de vue de la pratique pondérale, l’un des aspects les plus étonnants est l’extrême précision métrologique des premières pièces de monnaies qui dévie, pour certaines fractions les plus légères, de seulement 0,02 g de la valeur moyenne. Et si la frappe monétaire tend à formaliser plusieurs standards pondéraux, il est évident qu’une pesée de précision préexiste aux premières frappes. Selon A. Meadows et K. Shipton, le développement d’une pesée si précise ne peut être imputé qu’au besoin de mesurer des produits de forte valeur tels que le métal, les plantes ou certains produits transformés d’origine animale. Ils émettent ainsi l’hypothèse que l’apparition de la monnaie dérive d’une standardisation progressive des systèmes pondéraux et que l’argent-métal était utilisé comme monnaie au poids, sous la forme de lingot (silver bullion) avant l’invention de la pièce de monnaie63. De la même manière, Hans van Wees estime qu’une économie fondée sur le don peut se passer de standards métrologiques mais que la complexification et la contractualisation de la finance implique leur développement et tend vers l’universalisation du moyen de paiement comme des systèmes de mesure dans un soucis de facilitation des échanges64.
Cet attachement profond des questions de mesure pondérale et d’économie et leur lien inextricable dans un modèle évolutionniste aboutissant à la création de la pièce de monnaie est probablement légèrement surévalué. La raison à cela est multiforme et tient au moins en partie du fait que pour les périodes archaïques et postérieures, en ce qui concerne le monde de la Méditerranée centrale, ce sont essentiellement les numismates et les historiens de l’économie qui s’emparent du sujet de la métrologie pondérale. Cela est probablement en partie dû au fait que la création des poids comme celle de la monnaie sont attribuées pendant longtemps à Pheidon à Argos et à Solon à Athènes. Si leur rôle est surestimé, ils sont vraisemblablement à l’origine de réformes importantes65.
Pheidon règne sur Argos aux alentours du VIIe s. a.C. et a probablement créé ou réformé un système métrologique qui se répand ensuite rapidement dans le Péloponnèse66. Au début du VIe s. a.C., Solon, alors archonte, réforme ce système métrologique qui différencie d’un côté la pesée “commerciale” et de l’autre la pesée de l’argent (autrement dit la pesée d’un medium de paiement). La réforme en question est connue par deux commentaires, l’un d’Aristote (Constitution d’Athènes, 10) et l’autre d’Androtion (Atthis, Plutarque, Solon, 15.2 dans Harding 1994, F.34) dont les interprétations diffèrent. En substance, les deux commentaires indiquent que l’une des actions de la réforme est de faire passer le ratio mine/drachmes de 1 : 70 (selon Aristote) ou 1 : 73 (selon Androtion) à 1 : 100. Le sens des commentaires est cependant débattu quant à savoir s’il s’agit ici de l’imposition d’un rapport fixe entre système pondéral commercial et monétaire, d’une dévaluation de la drachme ou d’un alourdissement des standards pondéraux commerciaux67. Nous ne commenterons pas ce débat qui s’éloigne largement de notre domaine d’étude et de compétences mais nous noterons qu’il illustre bien les raisons de la relation forte entre économie et systèmes pondéraux pour tous ceux qui étudient la question. Toujours est-il que le fond de cette réforme est très certainement d’officialiser la mine d’argent à Athènes qui sert ensuite à l’élaboration du premier monnayage d’argent au milieu du VIe s. a.C. La mine rentre également dans le système pondéral “commercial”, dans lequel elle vaut la moitié d’un statère (qui reste structurant), au moins dès la fin du VIe s. a.C. La masse de cette mine d’argent ne change pas jusqu’à la période hellénistique68. Ainsi, on connaît pour Athènes une drachme estimée à 4,35 g, une mine de 435 g et une obole de 0,725 g69.
L’usage de deux systèmes pondéraux, l’un “commercial” et l’autre “monétaire”, se poursuit durant la période hellénistique. La mine devient cependant l’unité principale des deux systèmes et un décret stipule que les “poids commerciaux” sont applicables à tous les biens à l’exception de ceux qui doivent être payés en fonction d’un étalon-argent (Inscriptiones Graecae II/III 1013.29-37)70.
Pour le Levant, à la même époque, Gérald Finkielsztejn dresse une liste de sept étalons dont certains sont probablement la continuité des unités des âges du Bronze et du Fer. Dans les unités légères sont ainsi utilisés un shekel de plus de 11 g, la drachme attique de 4,35 g, le shekel de 9,3 g et une drachme phénicienne de 3,5 g associés à des mines “classiques” de 556,8 g, 504-515 g et 465 g. On trouve aussi des shekels et mines “lourds”, respectivement d’environ 12 g, 13 g, 7,5/15 g, 17 g et 600 g, 650 g, 750 g et 800-850 g71. Les relations arithmétiques qui lient ses différentes unités sont complexes et résultent vraisemblablement de nombreuses adaptations au cours du temps et l’existence d’unités “légères” et “lourdes” ne fait que les compliquer davantage.
Unités pondérales et unités monétaires
Sans rentrer complètement dans le détail, il est nécessaire de dire un mot sur le monnayage métallique tant les numismates ont eu un rôle prépondérant dans les études de métrologie. La question des monnayages métalliques amène encore un peu plus de complexité aux systèmes métrologiques en raison de l’introduction dans les équations des rapports de valeur entre les différents métaux. Le besoin de peser en fonction de standards métrologiques et de standards monétaires précis entraîne nécessairement une adaptation, au moins partielle, des instruments de mesure. Il devient en effet nécessaire d’adapter les systèmes métrologiques en vigueur aux masses des monnaies, au moins dans le cas d’une circulation de frappes exogènes. Cette adaptation est multiforme et dépend bien entendue du socle métrologique existant dans chaque contexte. Dans certains cas, il peut être nécessaire d’étendre l’intervalle de mesure de l’appareil pondéral. Dans le cas de la péninsule Ibérique, par exemple, les premières pièces de monnaie sont frappées dans des colonies grecques et en particulier celle d’Emporion vers le milieu du Ve s. a.C. Ces monnaies sont alors uniquement des fractions de divers étalons monétaires mais dont la masse n’excède jamais 1 g72. Or, comme nous le verrons plus en détail par la suite, il n’existe pas à cette époque en péninsule Ibérique de poids de balance permettant de mesurer des masses aussi faibles. Ainsi, l’appareil pondéral ibérique et l’appareil monétaire grec se retrouvent incompatibles et seule l’adaptation de l’un ou de l’autre peut permettre de les faire entrer dans un cadre d’utilisation commun. Dans d’autres cas, c’est le standard métrologique de l’un qui va devoir s’adapter à l’autre. Nous avons plus haut évoqué le cas de la Grèce où les premières frappes monétaires dénotent l’utilisation de standards pondéraux locaux rendant les pièces de monnaies émises métrologiquement incompatibles les unes aux autres. Il s’agit ici du cas où les premières frappes monétaires sont adaptées aux standards métrologiques locaux, cependant, dans d’autres cas, ce sont les standards métrologiques qui s’adaptent aux étalons monétaires déjà en usage. En Europe occidentale, l’articulation de ces phénomènes est particulièrement mal connue, notamment en raison de la méconnaissance des systèmes pondéraux antérieurs à l’introduction de la monnaie. Il est cependant évident que l’intégration d’étalons monétaires amène de nouvelles variables dans le champ de la pratique métrologique.
Du point de vue métrologique, les études numismatiques permettent de mettre en évidence des unités métrologiques généralement non renseignées par les textes ni par les poids, bien que les légendes monétaires puissent nous renseigner sur leurs dénominations. C’est par exemple le cas du système phocéo-phénicien, qui serait introduit par les Phéniciens à Carthage puis par les Phocéens à Marseille à partir du VIe s. Celui-ci s’appuie sur un shekel de 7,60 g à Carthage abaissé à 7,20 g en péninsule Ibérique73. Les émissions d’argent de Rhodé, Emporion et Gadès se distingueraient par l’utilisation d’une drachme d’environ 4,70 g74. En Gaule, les premières imitations locales sont d’abord de strictes imitations du statère de type Philippe II de Macédoine qui évoluent ensuite en des prototypes réellement locaux75. Cependant, les émissions monétaires ne correspondent pas à des standards pondéraux, elles dépendent de l’inflation et de la dévaluation ainsi que des pratiques locales, et ainsi, pour un même alliage, leur masse est susceptible de changer dans le temps et dans l’espace, comme le montre l’exemple flagrant des monnaies à la croix frappées à partir de la fin du IIe s. a.C.et dont la masse est comprise entre 0,5 et 3,676.
En péninsule Ibérique les premières frappes monétaires “indigènes” sont frappées à Arse-Saguntum dans la seconde moitié du IVe s. a.C., s’appuyant sur des standards métrologiques de 3,4 et 2,6 g semblables aux émissions d’Ebusus77, mais restent longtemps un épiphénomène. Dans le reste de la péninsule, comme en Gaule méridionale, il faut attendre le milieu ou la fin du IIIe s. a.C. pour voir une réelle adoption de l’appareil monétaire, une chronologie généralement interprétée comme la conséquence du renforcement des contacts avec les Carthaginois pour la péninsule et avec la Méditerranée pour la Gaule78. Les premières émissions à légendes ibériques sont des deniers qui apparaissent dans le nord-est de l’Espagne, ils sont tout d’abord alignés sur le denier romain (3,89/3,94 g) mais à la fin du IIe et début du Ier s. a.C., certaines émissions accusent une diminution de leur masse79. Au IIIe s. a.C., il semble que Marseille se mette également à frapper des monnaies alignées sur une métrologie romaine (le victoriat léger de 2,88-2,91 g)80 alors qu’ailleurs, comme par exemple sur la rive gauche du Rhône, on connait plusieurs standards monétaires auxquels il est difficile d’attribuer une paternité81. Jean-Claude Richard et Leandre Villaronga, concernant les émissions d’argent de la péninsule Ibérique et de la Gaule du Sud entre les VIe et Ier s. a.C., distinguent quatre systèmes métrologiques principaux : celui de la litre sicilienne (une lourde de 1,164 g et une légère de 0,87 g avec des oboles respectives de 0,97 g et 0,72 g), le système phocéo-phénicien construit sur un shekel de 7,2-7,6 g, un possible système hispanique avec une unité de 4,9 g et enfin le modèle romain avec notamment des émission s’alignant sur le quadrigatus de 6,72-6,84 g82. Pour les émissions de bronze, les types sont plus nombreux, mais la métrologie romaine prédomine selon les auteurs au sein duquel on peut noter une unité de 8,7 g83. Plus qu’une liste d’unités métrologiques propres aux émissions monétaires qui, en regard de l’aire géographique prise en compte ici serait bien longue, nous noterons que dans leur étude, l’une des observations de conclusions qu’émettent J.-C. Richard et L. Villaronga est que, dans le contexte de luttes importantes qui marquent la période d’adoption de l’appareil monétaire, il semble que les métrologies adoptées soient généralement alignées sur celles des groupes dominant les régions émettrices84.
Les données issues de la numismatique, bien que riches en informations, ne sont donc pas toujours les meilleures sources pour appréhender directement la métrologie pondérale. Il est cependant assez bien admis que dans un premier temps, les monnaies diffusées en Europe occidentale sont employées pour leur valeur intrinsèque en termes de quantité de métal. Leur valeur faciale, directement liée à la garantie que représente la frappe, semble écartée. Par conséquent, si l’objet lui-même est potentiellement utilisé comme monnaie, il ne l’est pas nécessairement comme “monnaie frappée”, dans le sens qu’englobe le terme anglais “coinage”85. Si l’objet-monnaie est traité comme une masse de métal et non pas comme une unité de valeur, alors cela signifie que le rapport direct entre pièce de monnaie et valeur n’existe pas.
L’usage d’un appareil monétaire exige qu’au moins une partie du système pondéral employé soit adapté à la pesée des émissions monétaires. Si cette pesée n’est certes pas systématique, elle est toutefois indispensable lors de la frappe et afin d’enrayer les tentatives de fraude. Dans les premiers temps de la circulation de pièces de monnaie en Europe occidentale, l’absence d’assimilation directe entre pièce de monnaie et unité de valeur semble indiquer qu’un tel processus d’adaptation est encore inexistant. Il est fort probable que cette situation change dès lors que la monnaie commence à être frappée localement, soit que les systèmes métrologiques s’adaptent pour partie ou totalement à des masses d’émissions allochtones, soit que les monnaies soient alignées sur des unités pondérales locales.
II. L’Europe continentale :
la naissance d’une “métrologie archéologique”
Au cours des XIXe et XXe s., l’engouement pour la métrologie ancienne concerne essentiellement l’étude des populations de la Méditerranée centrale et orientale pour lesquelles nous connaissons des textes mentionnant unités et systèmes métrologiques. L’étude des instruments de mesure eux-mêmes reste anecdotique et sert essentiellement à illustrer une démarche de “métrologie historique”. La méthode se veut essentiellement comparative et vise à chercher dans le registre archéologique les unités mentionnées dans les textes. Le lent développement de ces recherches possède un écho réduit dans la recherche archéologique protohistorique. Si l’existence ancienne d’une pratique pondérale chez les populations méditerranéennes est évidente, une telle assertion ne semble pas partagée pour les peuples des âges du Bronze et du Fer en Europe occidentale.
1. Les palafittes et les Terramare :
les premières recherches de métrologie en Europe
Le contexte de la fin du XIXe s. se prête assez mal à un questionnement sur l’existence d’une métrologie autre que celle du Monde Classique, c’est pourtant à cette époque qu’apparaissent les premières mentions de poids de balance antérieurs à l’Antiquité. La plus ancienne que nous connaissons est celle de Victor Gross, un médecin et antiquaire suisse qui s’intéresse tout particulièrement à la Préhistoire des sites lacustres. Il décrit en 1883, dans Les Protohelvètes, une “pierre arrondie et bien polie, munie au sommet d’une boucle en bronze, qui apparemment servait de poids” (fig. 1-7). Il compare alors celle-ci à une série de pierres polies discoïdes réalisées à partir de matériaux lithiques durs présentant des dépressions sur chaque face et une rainure périmétrique (fig. 1-8)86. Bien que l’identification exacte que V. Gross met derrière le mot “poids” reste assez floue (poids de filet, de métier à tisser, de balance…), il reste qu’il identifie alors ce qui apparaît encore aujourd’hui comme les deux grandes catégories de poids de balance des sites lacustres alpins du Bronze final.
La fin du XIXe s. est une période de profond questionnement scientifique sur les modes de développement des populations préhistoriques, entre “Antiquités Nationales” et diffusionnisme, de définitions de phasages chronologiques émancipés des considérations historiques. Au sein de ces questionnements interprétatifs, seule une petite partie du mobilier archéologique fait réellement l’objet d’une attention scientifique. V. Gross, s’il mentionne les pièces, ne semble alors accorder que peu d’intérêt à la place de ces objets dans la vie quotidienne et ne s’interroge pas outre-mesure sur leur fonction. De plus, les concepts chrono-culturels sont encore assez mal définis et peu harmonisés à l’échelle de l’Europe87.
C’est ainsi Robert Forrer, antiquaire et archéologue d’origine suisse, longtemps conservateur bénévole du Musée préhistorique et gallo-romain de Strasbourg, qui parle le premier d’une “métrologie préhistorique” pour l’Europe88. Il livre un important travail basé sur l’étude de poids métalliques découverts dans les stations lacustres de l’âge du Bronze. De ces artefacts il déduit l’existence d’une “mine lacustre” de 735 g utilisée parallèlement à une mine phénicienne de 728 g, une mine crétoise-éginète de 618 g, peut-être une mine babylonienne de 505 g et une mine égyptienne de 409 g89. Son étude va plus loin en tentant de mettre en relation ces unités avec la pesée des métaux au travers du matériel en argent, en or et en fer issus de contextes chronologiques et géographiques variés (pour ne pas dire différents)90. Le travail de R. Forrer est d’une grande importance pour l’étude de la métrologie ancienne bien qu’il s’ancre complètement dans les théories comparatives et diffusionnistes qui caractérisent alors une grande partie du débat scientifique.
En 1917, la découverte d’un nouveau poids à Strasbourg (Alsace, France ; notre objet Stras-A) l’amène à rédiger une nouvelle notice sur le sujet qui est publiée en 192391. Le poids en question est en pierre et de forme globulaire, sur son sommet se trouvait vraisemblablement un anneau de suspension métallique aujourd’hui disparu. Métrologiquement, R. Forrer le rapproche, ainsi que celui de Port (Pt-A), de morphologie similaire, d’une mine égyptienne de 546 g. Celle-ci aurait déjà été adoptée précocement en Italie, ce qui amène R. Forrer à conclure que “nos lacustres n’ont pas emprunté directement cette mine aux Égyptiens, mais à quelque intermédiaire plus proche d’eux”92. Peu de temps après, Joffroy Bergthol rapproche un objet trouvé sur le Mont Hérapel (Cocheren, Moselle, France ; MHer-A) des poids identifiés par R. Forrer. Selon lui, celui-ci correspond “exactement” au cinquième d’une mine carthaginoise de 392 g (après une augmentation de 10 % de la masse de l’objet pour corriger son usure) également représentée à Colombier (Neuchâtel, Suisse ; Col-A) et Vallamand (Vully-les-Lacs, Vaud, Suisse ; Vall-A).
Dans les années qui suivent, les poids de balance lacustres semblent tomber en désuétude et disparaître du paysage archéologique, tout comme l’idée d’une métrologie pondérale de l’Europe moyenne pré- ou protohistorique. La faute est peut-être due à une absence de découvertes de vestiges de ce type ou à un désintérêt pour ces considérations. La seule exception est cette fois-ci française, puisqu’en 1937, l’abbé Philippe dédie une partie de ses mémoires sur les fouilles du Fort-Harrouard (Sorel-Moussel, Eure-et-Loir, France) à la question du commerce et du système pondéral utilisé sur le site. Il identifie alors trois poids de balance globulaires ou piriformes (FH-A, FH-D et FH-E), respectivement en pierre (et bélière sommitale en alliage-cuivreux), en alliage cuivreux et en plomb. Pour lui, le poids FH-A se rapproche par son type et par sa masse des poids et systèmes métrologiques des sites lacustres mais différerait légèrement en raison de variations locales93.
2. La quête du métal pesé
Un thème récurrent des recherches en Protohistoire est la théorie qu’une partie ou la totalité des processus d’échanges se faisaient au moyen de métal présentant une certaine forme de calibration, avec l’idée induite ou explicite, que celle-ci est effectuée au moyen d’une pesée. L’hypothèse est fortement ancrée et on la retrouve dans la littérature scientifique à partir de la fin du XIXe s. Cette association entre pesée et commerce fait long feu, en Protohistoire européenne et ailleurs, et la pratique pondérale est parfois annoncée comme une étape dans l’évolution de l’économie et du commerce dont l’achèvement serait caractérisé par l’apparition de la pièce de monnaie94.
Les premières mentions de métal pesé
L’une des premières occurrences, si ce n’est la première, de la mention de métal pesé pour l’Europe occidentale protohistorique, est le fait d’Édouard Desor, zoologue et géologue avant de s’intéresser à la Préhistoire. Il présente à la société des sciences naturelles, dès 1870, ce qu’il interprète comme un “porte-monnaie lacustre”. L’auteur propose de voir des monnaies dans certains bracelets utilisés à l’âge du Bronze sur les sites lacustres. L’un de ses principaux arguments est la découverte d’un lot de bracelets de dimensions similaires rassemblés par un autre anneau ouvert, en étain (fig. 1-9). D’autres exemplaires semblables sont découverts régulièrement dans les sites lacustres suisses, l’anneau d’assujettissement y est parfois en alliage cuivreux95. L’idée est fortement critiquée plusieurs années plus tard par Arnold Morel-Fatio, un numismate très actif en France et en Suisse, qui rejette l’adhésion de ces objets à la définition de la monnaie en tant que “pièce de métal servant aux échanges, frappée par une autorité souveraine et marquée au coin de cette autorité”. Selon lui, tous les échanges sont effectués “en nature” à l’âge du Bronze et les bracelets en question présentent des qualités métalliques et des masses variables. Il reconnait toutefois avoir lui-même trouvé de nombreux anneaux reliés entre eux par “une bande plate d’un métal extrêmement mince” souvent disparu par manque de soins96.

En 1888, Jules Pilloy, archéologue amateur dans l’Aisne, écrit à propos des fragments métalliques du dépôt de Brécy (Aisne) que “chacun des morceaux, dont la brisure avait été faite intentionnellement, avait un poids sensiblement uniforme, ce qui semblerait faire croire que l’on pouvait s’en servir comme monnaie courante.”97.
Quelques années plus tard, le numismate Jules Adrien Blanchet, écrit l’article au titre explicite : “le bracelet considéré comme moyen d’échange antérieur à la monnaie frappée”. Dans cette note, il expose certaines comparaisons historiques et ethnographiques pour indiquer que les anneaux intègrent “souvent” la double fonction de bijoux et de moyens d’échanges. Il remarque cependant qu’en Europe, aucune relation arithmétique n’indique l’usage d’un système pondéral dans la confection de ces objets98.
Il reprend le dossier des “monnaies primitives” quelques années plus tard dans son “Traité des monnaies gauloises”99. Son propos reste cependant assez descriptif et peu conclusif. Il cite un certain nombre de découvertes de haches, de parures annulaires et de rouelles, généralement trouvées en contexte de dépôt, qui pourraient avoir servi de monnaies. Cependant, il estime qu’en l’absence de pesées systématiques, il est impossible de conclure sur le sujet.
Entre temps, en 1901, Henry de Gérin-Ricard écrit un court article sur les monnaies-parures, deux composantes qui sont selon lui indissociables. Il dresse une liste de ces dernières : les coquilles, les monnaies obéliennes (ou monnaies-lingots) et les monnaies annulaires. Il déclare notamment que le métal pesé est utilisé comme monnaie sous la forme de haches en Gaule que ce soit dans la région méditerranéenne ou dans le nord-ouest du territoire. Quant aux parures annulaires en alliage cuivreux trouvées en Europe pour l’âge du Bronze, l’auteur estime qu’elles ont également pu “servir de base à des transactions commerciales”100.
Joseph Déchelette : instruments de pesée
et métal pesé entre Méditerranée et Europe
Les travaux de R. Forrer semblent avoir une grande influence sur Joseph Déchelette qui, lorsqu’il écrit son Manuel d’Archéologie prehistorique, celtique et gallo-romaine, consacre une place importante à la question des pratiques pondérales et du métal pesé, en particulier dans les tomes consacrés à l’âge du Bronze101 et à la période de La Tène102.
De manière synthétique, l’hypothèse avancée par J. Déchelette, en se fondant notamment sur une comparaison avec des phénomènes observés en Méditerranée centrale103, est que les populations de l’Europe de l’âge du Bronze utilisent du métal pesé comme moyen de paiement.
Selon lui, les haches découvertes en contexte de dépôt en Bretagne et en Normandie pour la fin de l’âge du Bronze serviraient à la fois d’outils et de “monnaies primitives”. Les principaux arguments qu’il avance sont la faible épaisseur d’un certain nombre d’exemplaires, trop minces ou trop petits pour avoir servi d’armes ou d’outils (ex : dépôts de Plurien, Côtes-d’Armor ; dépôt de Maure-de-Bretagne, Ille-et-Vilaine), les haches reliées par des fils métalliques (ex : Kergrist-Moëllou, Côtes-d’Armor), les haches en plomb de Bretagne et les objets fragmentés aux masses similaires (ex : Brécy, Aisne). Cette dernière hypothèse est déjà envisagée avant lui par J. Pilloy et J. A. Blanchet. Concernant l’usage d’instrument de pesée, il explique que “le commerce avait acquis à l’âge du Bronze un grand développement non seulement chez les peuples méditerranéens, mais encore parmi toutes les tribus de l’Europe occidentale, centrale et nordique. A priori, cet état de choses implique presque nécessairement l’usage d’un système de poids et de mesures.”104.
Selon J. Déchelette, l’usage de haches comme medium de paiement renvoie à une tradition ancienne qui dérive de la circulation en Méditerranée de lingots en “peau de bœuf” en cuivre qu’il décrit comme des “saumons de forme bipenne”. La forme générale se serait conservée alors que la morphologie même de l’objet aurait évolué105. La forme de double hache (les lingots en peau de bœuf) évoluerait vers la hache simple (demi bipenne) en Europe occidentale. À la fin de l’âge du Bronze et au Premier âge du Fer, d’autres objets pourraient prendre la même fonction, tels que les anneaux, les rouelles et les bracelets avant d’être progressivement remplacés par la monnaie à proprement dite (coinage)106. Un argument en faveur de cette dernière hypothèse est alors l’utilisation du motif des “rouelle-amulettes” sur des monnaies grecques d’époque archaïque, notamment celles en relation avec les zones celtiques, l’Italie du sud et la Sicile, et qui finit par être emprunté par les Gaulois107.
Du point de vue de ses références et de son analyse, J. Déchelette est relativement imprégné de l’école allemande de “métrologie comparative” initiée par A. Böckh108 et il s’appuie notamment sur les travaux de F. O. Hultsch109. Il s’avère cependant beaucoup plus prudent que ces derniers lorsqu’il s’agit de comparer des unités métrologiques et il explique ainsi que “comme l’oxydation du plomb a pu altérer les poids des palafittes et que, d’autre part, la métrologie des peuples de l’antiquité orientale et gréco-latine présente encore maintes obscurités – les chiffres proposés par les auteurs les plus autorisés ne concordant pas tous – la recherche de l’origine du système pondéral des Ligures peut difficilement aboutir à des résultats bien précis.”110. Ses propositions métrologiques restent donc réservées et il se contente généralement de mettre en avant des relations pondérales directes comme par exemple entre certains exemplaires de haches et le poids en plomb d’Onnens (fig. 1-10)111.

d’après Déchelette 1910, 405.
Entre monnaie et pesée : paléomonnaies, prémonnaies,
lingots et métal pesé
Au début du XXe s., l’idée d’une pratique pondérale protohistorique est bien assimilée et elle se mêle progressivement à celle de l’usage d’une “monnaie non frappée” en métal pesé. On peut ainsi percevoir un certain glissement de différents concepts qui tendent à se mêler autour d’une idée générale de métal calibré, qui est parfois défini comme une “paléomonnaie” ou une “prémonnaie” ou parfois comme un lingot. Au milieu de cet imbroglio conceptuel, il n’est pas toujours très clair de savoir si, selon les auteurs, les objets considérés sont calibrés par leur masse ou non. Lorsque cette dernière hypothèse apparaît de manière relativement explicite, c’est la chaîne opératoire qui ne l’est pas toujours. Cela signifie qu’il n’est pas toujours signifié s’il s’agit d’un objet dont la masse de métal de conception a été pesée ou d’un objet fini dont la masse a été vérifiée et/ou ajustée. Le même problème se pose dans le cas des objets fragmentés : la chaîne opératoire diffère selon qu’on considère qu’un objet est fragmenté afin que sa masse s’intègre dans un intervalle acceptable ou bien que l’on tente d’obtenir une masse définie par fragmentation. De l’assimilation de ces concepts découle une vision linéaire amenant à interpréter les dépôts comme des dépôts monétaires et donc leur contenu comme de la monnaie, qui par conséquent est un métal calibré, sous-entendu pesé.
En Europe occidentale, plusieurs zones géographiques sont alors la cible de ce manque de clarté qui, s’il n’est probablement pas partagé par tous, ne semble jamais réellement tranché : la Bretagne avec ses dépôts de haches, l’aire des dépôts launaciens et la Grande-Bretagne avec les currency bars. Mais le flou qui entoure les concepts évoqués est probablement la cause du manque de publications discutant clairement la question du métal pesé au cours du XXe s. Certains auteurs évoquent clairement l’hypothèse de constructions pondérales, tel Bénard le Pontois 1929 qui restitue pour les haches armoricaines un système construit autour d’une unité (296 g) et de ses sous multiples (79 g, 36-37 g)112. Mais de manière générale, il semblerait que les questions liées à la masse des objets métalliques tendent à disparaître des problématiques de recherche au cours du XXe s.
La question des currency bars britanniques est à peine plus explorée. L’interprétation économique faite par Réginald Smith au début du XXe s. et qui leur donnera leur nom repose sur un passage de la Guerre des Gaules où César décrit l’usage de masses métalliques en fer pesé comme monnaie (Guerre des Gaules, 5.12)113. L’étude de R. Smith, qui s’appuie alors sur les exemplaires conservés au British Museum montre une possible standardisation pondérale des barres de fer en question ce qui l’amène à les interpréter comme les formes de monnaie dont parle César. Le réexamen du dossier plusieurs décennies plus tard par Derek Allen montre que la question n’est pas si simple et que des différences régionales existent. Cependant l’auteur admet qu’au moins une partie des barres de fer en question sont standardisées selon leur masse et possèdent une fonction monétaire. En revanche, il indique qu’aucune donnée ne va dans le sens d’une construction pondérale similaire sur le continent114.
La question de l’existence et de l’utilisation d’une paléomonnaie dans l’Europe protohistorique a été discutée par Jacques Briard à de nombreuses reprises à partir des années 1980115. Si la fonction des haches à douilles armoricaines comme support monétaire ne fait guère de doute pour lui, leur régularité est, selon lui, plus probablement à chercher dans leur forme et leur taille que dans leur masse bien que celle-ci soit relativement constante116. Il émet des conclusions similaires concernant les dépôts launaciens, ainsi nommés en 1902 par Paul Cazalis de Fondouce suite à la publication du dépôt de Launac (Hérault) et amplement étudiés postérieurement, notamment par Jean et Odette Taffanel117 et Jean Guilaine118.
Une autre contribution à la thèse de l’utilisation de métal pesé en Europe protohistorique est celle que Mansel Spratling consacre à la pesée de l’or en 1980. L’auteur s’attarde réellement sur les masses des objets pour argumenter en faveur d’un véritable contrôle pondéral de ces derniers. Certains exemples donnés sont intéressants, comme la parure en or du dépôt de Féregyháza (Bánság, Roumanie) qui présente de réelles concentrations de masses (fig. 1-11). Cependant, l’auteur compare des objets parfois très éloignés dans le temps et dans l’espace et son échantillonnage est loin d’être systématique119. Par conséquent il est difficile de prendre les résultats de M. Spratling au pied de la lettre et d’adhérer à ce qui semble être l’adoption d’un standard pondéral européen pour la pesée de l’or.
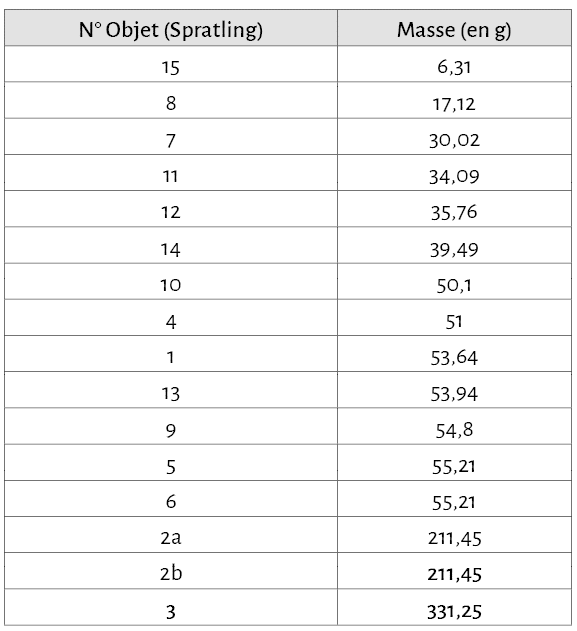
d’après Spratling 1980.
Entre la fin des années 1990 et le début des années 2000, Majolie Lenerz-de Wilde effectue des recherches systématiques sur la normalisation par la masse en Europe centrale entre le Chalcolithique et l’âge du Bronze ancien. Elle émet notamment l’hypothèse de l’existence d’une monnaie primitive fondée sur un système pondéral qui évoluerait et se construirait dans le temps. Selon l’auteure, les torques en cuivre, tout d’abord utilisés pour leur simple fonction de parure (Bz A1a) sont progressivement standardisés comme des lingots puis utilisés comme forme de monnaie (Bz A1b). La normalisation pondérale de lingots plus légers deviendrait ensuite commune (Bz A2a-b). Ces torques-lingots en cuivre sont alors souvent trouvés reliés entre eux par “grappe” de cinq (fig. 1-12). Une transition aurait ensuite lieu avec le dépôt de formes de lingots miniaturisés très légers et des fragments de lingots entre la fin du Bz A et le début du Bz B (soit la fin du XVIIIe-début du XVIIe s. a.C.). Les pratiques antérieures laisseraient ensuite place à un nouveau système de monnaie s’appuyant sur des fragments de métal sous forme de matière première ou d’objets fragmentés qui perdurerait ensuite jusqu’à la fin de l’âge du Bronze120.

L’hypothèse de l’utilisation en Europe centrale à l’âge du Bronze d’un medium de paiement constitué par du métal fragmenté a été émise à de nombreuses reprises. Plusieurs auteurs suggèrent ainsi que des chutes de métal ou des lingots sont intentionnellement découpés afin de correspondre à une calibration pondérale. R. Peroni identifie par exemple trois séries fondées sur des systèmes pondéraux dans des dépôt italiens de l’âge du Bronze ancien et moyen qui correspondent selon lui à des unités de 190-200 g et 270-300 g pour la première, 63 g pour la deuxième et 26 g pour la dernière121. Il ne publie cependant pas les données détaillées qui lui permettent d’arriver à ces résultats, ce qui rend ses résultats difficilement exploitables.
Le sujet du métal fragmenté comme support d’échange a également intéressé l’archéologue suisse Margarita Primas. En Europe centrale, elle suggère l’existence d’une calibration et graduation des masses d’un ensemble d’anneaux et de spirales en or datés des IVe et IIIe millénaire a.C., trouvés dans les Balkans dans la tombe de Reka Devnja (Varna, Bulgarie), à Ampoița (Alba, Roumanie) et à Velika Gruda (Montenegro). Elle n’estime cependant pas qu’il s’agisse là de la preuve de l’utilisation d’un système métrologique mais peut-être d’une simple balance122. Josef Eiwanger, en revanche, suggère l’existence d’une unité pondérale pour l’or durant le Chalcolithique. Il reconstruit celle-ci à partir de la masse des objets de la nécropole de Varna (Bulgarie) et l’établit, avec un degré de précision peu à propos, à 0,935657 g123.
Mais selon M. Primas, c’est aux alentours de 1350 a.C. que le métal pesé devient réellement une forme de monnaie (currency). Plusieurs arguments l’amènent à ce constat :
- la fragmentation volontaire d’objets finis tels que les faucilles en alliage cuivreux124 en parts homogènes ou en multiples d’une unité pondérale basique ;
- la régularité des masses de certains objets aux formes standardisées comme les haches et les faucilles ;
- l’ampleur de l’aire de circulation des lingots de cuivre, comme les lingots en peaux de bœuf trouvés dans les dépôts du sud de l’Allemagne ;
- les premières utilisations de symboles écrits attestées par les tablettes en bois trouvées dans les mines de sel de Kitzbuehel dans les Alpes125.
Par conséquent, même si l’historiographie présentée ici n’est pas exhaustive, elle permet de constater que les études abordant le thème du métal pesé au cours du XXe s. sont inégales et peu étayées par de réelles analyses pondérales. Le sujet est généralement déconnecté de celui des outils de mesure et repose sur l’idée que des formes de monnaie apparaissent au Chalcolithique ou à l’âge du Bronze, prenant la forme de métal découpé, calibré et/ou pesé, sans que la différence n’apparaisse clairement.
“Paléomonnaie” et systèmes de pesée :
les travaux de Marisa Ruiz-Gálvez
Depuis les années 1990, Marisa Ruiz-Gálvez a consacré plusieurs travaux sur la question de l’économie protohistorique et notamment du métal pesé et des systèmes pondéraux dans une approche très globalisante qui tend à s’opposer à la vision d’une Europe protohistorique isolée de la Méditerranée portée selon elle par l’archéologie processualiste126. En mêlant un certain nombre d’études personnelles et de résultats de travaux antérieurs, l’auteure s’est attachée à retrouver dans le corpus archéologique les traces de systèmes pondéraux attestant à la fois de la pratique de standardisation pondérale de produits finis métalliques mais surtout la diffusion paneuropéenne d’unités d’origine méditerranéo-orientale.
Elle reprend notamment les travaux menés par Mats Malmer et Erik Sperber sur la Scandinavie127 et propose de voir dans le système nordique une origine égéenne. Selon elle, il serait construit sur une unité de 6,7 g et un système de comptage binaire. L’identification du même système en Europe centrale par J. Eiwanger128 lui permet de tracer son utilisation le long de la “Route de l’Ambre” qui relie commercialement la Méditerranée à l’Europe du Nord, prouvant ainsi des échanges de personnes, de biens et de connaissances129.
Elle identifie cette même unité égéenne au sud de l’Espagne, dans le trésor de Villena d’après l’étude de la masse des objets complets en or (bracelets et éléments de vaisselle). Elle n’y voit pas une relation directe entre Mycènes et la péninsule Ibérique mais plutôt la marque d’une route commerciale post-mycénienne qu’elle relie à la présence chypriote en Sardaigne. Le dépôt n’a cependant pas de contexte archéologique datable130.
Un autre système pondéral que M. Ruiz-Gálvez identifie en Europe occidentale est celui basé sur un shekel “microasiatique” de 11,75 g, que C. Zaccagnini juge très répandu à Chypre et dans le Levant131. Elle détecte cette unité dans les dépôts de types “Sagrajas-Berzocana” en péninsule Ibérique, composés de torques et de bracelets en alliage cuivreux et en or, datés entre le XIe et la deuxième moitié du IXe s. a.C.132. Le même système serait également à l’origine, selon elle, de la constitution des torques de type Tara-Yeovil trouvés en Irlande, en Grande-Bretagne, en France et en Espagne. P. Northover avait déjà mis en évidence la construction pondérale de ces objets selon des modalités régionales133. Enfin, les bracelets du dépôt de Flumenelongu et les lingots de plomb de Santa Anastasia di Sardara, en Sardaigne, seraient eux aussi calibrés sur des multiples d’une unité de 11,75 g134.
Une troisième unité d’origine méditerranéenne est selon M. Ruiz-Gálvez présente en Europe occidentale : un shekel dit “phénicien” d’environ 7,5-7,9 g (le shekel “de Karkemish” de 7,83 g cité plus haut). Le système pondéral découlant de cette unité serait visible dans le trésor de Caldas de Reyes (Galicia, Espagne), daté de la transition Bronze final-Premier Fer en raison de la présence d’objets produits selon la technique de la cire perdue135, ainsi que dans les haches riches en plomb de Galice et du nord du Portugal136.
Le même système pondéral préside selon elle la fabrication des haches armoricaines puisque les masses mise en évidence par Bénard de Pontois137 et citées par Briard peuvent correspondre aux multiples 5 : 10 : 20 : 35 : 40 d’un shekel de 7,9 g. Cependant, ce dernier auteur indique bien que la construction observée résulte de divergences régionales et non d’une véritable construction pondérale138 ce qui rend l’hypothèse caduque.
Les travaux de M. Ruiz-Gálvez, s’ils ne manquent pas d’intérêt et de réflexions sur la teneur des relations paneuropéennes, montrent toutefois des biais certains. La recherche constante d’unités méditerranéennes découle de l’idée, assumée par l’auteure, que dans le cadre de relations commerciales appuyées, les populations de l’Europe occidentale vont adopter les standards pondéraux les plus utilisés. Cependant, une telle démarche repose sur le préjugé indémontré que ces populations n’ont pas déjà une pratique pondérale et des standards qui leurs sont propres. De plus, les études sur la métrologie pondérale de la Méditerranée orientale à l’âge du Bronze montrent qu’il est bien difficile de parler de standards étalons pour cette époque tant elle se caractérise par une souplesse et une navigation constante entre plusieurs systèmes arithmétiques interconnectés. Il semble donc nécessaire aujourd’hui de confronter les hypothèses énoncées à des méthodes d’analyses non diffusionnistes afin d’en éprouver la solidité.
3. Une première vision d’ensemble
des pratiques pondérales européennes
Il faut attendre la fin des années 1990 pour que commence à se dégager l’image d’une véritable pratique pondérale en Europe occidentale. Les travaux qui vont voir le jour s’appuient en grande partie sur les identifications et les études menées antérieurement par V. Gross139, R. Forrer140, M. Malmer141 ou M. Lenerz-de-Wilde142.
Nous pouvons distinguer trois apports principaux à cette nouvelle métrologie archéologique de l’Europe occidentale : les travaux menés par une équipe italienne dirigée par Andrea Cardarelli sur les poids de balance de l’âge du Bronze mis au jour dans les Terramare143, la synthèse de Christopher Pare sur les pratiques pondérales en Europe centrale au Bronze final144 et l’identification des premiers fléaux de balance en Europe occidentale pour la même période par Rebecca Peake, Jean-Marc Séguier et José Gomez de Soto145.
Les Terramare
La fin des années 1990 a vu la publication d’un ensemble d’objets en pierre, issus essentiellement de la région des Terramare, autour de la vallée du Pô, entre le Bronzo Medio 3 et le Bronzo final146 (soit entre le XIVe et le milieu du Xe s. a.C.). Leur forme atypique amène A. Cardarelli et son équipe à les interpréter comme des outils pondéraux. L’étude s’appuie sur l’identification de deux types d’objets lithiques à la morphologie singulière : un premier type de forme lenticulaire disposant d’une rainure périmétrique et un deuxième piriforme muni d’une protubérance sommitale généralement perforée et faisant office de bélière (fig. 1-13)147.
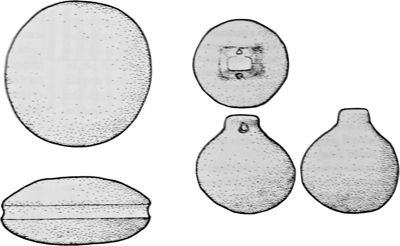
Les auteurs proposent de les identifier comme des poids de balance sur la base de plusieurs critères : le soin apporté à leur fabrication, l’existence d’exemplaires de dimensions distinctes dont certains de petite taille et bien évidemment leur analyse pondérale148. Cette dernière est structurée autour de la mise en évidence de convergences ou de concentrations de valeurs pondérales, ainsi que de la constance des intervalles qui les séparent et des relations arithmétiques entre les différentes valeurs ainsi isolées. La méthode repose donc en grande partie sur l’observation d’histogrammes de répartition des valeurs149 et leur “oscillation” autour de valeurs moyennes (fig. 1-14).
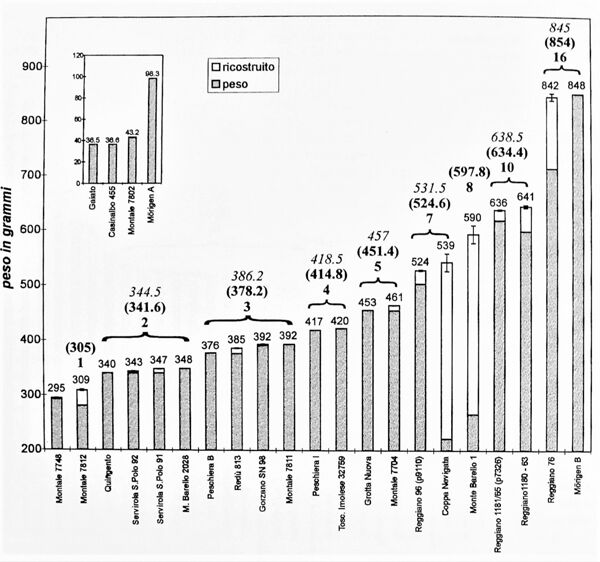
Les auteurs mettent ainsi en évidence plusieurs unités possibles pour ces deux groupes d’objets (fig. 1- 15). Les poids de forme lenticulaire sont, selon eux, organisés autour d’une unité d’environ 53,5 g représentée par des multiples 8 : 10 : 12 : 16150 alors que les poids piriformes à bélière semblent construits autour de deux unités : l’une de 6,1 g (ou 12,2 g) et l’autre d’environ 305 g égale à 50 fois la première151.

La comparaison avec des artefacts similaires trouvés en Suisse est mise en avant dès 1997 et développée quatre ans plus tard. Il est notamment bien mis en évidence que les exemplaires suisses possèdent une chronologie générale plus récente, centrée autour des XIe-IXe s. a.C.152. Les auteurs proposent un modèle de diffusion et d’adoption métrologique depuis l’aire égéenne dont les systèmes métrologiques sont connus par les travaux de K. Petruso153. Selon eux, les unités observées dans les Terramare puis dans les sites lacustres suisses, correspondraient à l’adaptation des unités de 5,5 g (proche de 53,5 ÷ 10), 61-65 g (6,1 x 10) et 36,6 g154 identifiées dans le Bassin égéen.
L’ambition des auteurs est avant tout de présenter un corpus archéologique d’artefacts dont la normalisation pondérale est suspectée et de tenter de confirmer celle-ci en élaborant des outils efficaces pour le faire, comme l’observation de la distribution de leurs masses. Les résultats de cette démarche profondément archéologique sont ensuite comparés aux données disponibles dans les aires géographiques proches. Cette étude représente le premier jalon d’une démarche de métrologie archéologique en Europe occidentale qui tente, tout du moins dans son cadre d’analyse, de s’émanciper des influences de l’historiographie de la métrologie méditerranéenne.
Christopher Pare : la première synthèse
Dans la décennie 1990, le Römisch-Germanisches Zentralmuseum de Mainz procède à la restauration et l’analyse du mobilier découvert dans la tombe de Milavče (Bohème), qui a livré un petit chaudron à roues et une épée de type “Riegsee” du XIIIe s. a.C., conservé au Národní Muzeum de Prague. Au sein de cet ensemble, un petit parallélépipède en alliage cuivreux jusqu’alors peu étudié attire l’attention de Christopher Pare. Une comparaison avec d’autres découvertes permet de l’associer à une nouvelle catégorie de poids de balance. C. Pare s’empare alors du sujet en reprenant la documentation amassée sur le sujet par Ulrich Schaaff et Dietrich Ankner durant les trente années précédentes. Il publie les résultats de son analyse en 1999 dans les actes du colloque Eliten in der Bronzezeit sous la forme d’un imposant article qui fait, encore aujourd’hui, office de référence sur la question155.
Au travers d’un inventaire alors relativement exhaustif des instruments de pesée de l’âge du Bronze final (39 poids de forme rectangulaire ou sub-rectangulaire en alliage cuivreux ainsi que de trois balances ; fig. 1-16), C. Pare dresse une première synthèse des pratiques de pesée protohistoriques. La grande majorité des artefacts qu’il présente sont découverts en contexte funéraire, plus quelques-uns dans des habitats ou des dépôts, dans les territoires actuels de la République Tchèque, la Hongrie, l’Allemagne, la Suisse et la France156. C. Pare remarque que plusieurs d’entre eux sont déposés dans des contenants en matière périssable, soit des coffrets en bois dont il reste parfois des charnières métalliques soit des sacs textiles157. Selon lui, une partie du mobilier d’accompagnement des sépultures élitaires répond à des pratiques normalisées (chars, service à boisson, etc.), alors que le contenu de ces coffrets ou de ces sacs relève plus probablement de la sphère privée, ce qui expliquerait notamment l’hétérogénéité de leur contenu. En dehors des instruments de pesée, il définit ainsi six autres catégories principales d’objets présents dans ces contenants personnels : des objets du quotidien, des instruments de toilette, du matériel lithique varié, des matières premières, du mobilier d’habillement ou de parure et certains objets exotiques158.

M. Primas (7-9), A. Beck (13)).
Pare dresse un parallèle entre le dépôt funéraire d’instruments de pesée en Europe centrale et dans le monde égéen. Les deux pratiques partagent un certain nombre de traits communs dont le statut social élevé des individus enterrés avec des poids ou des balances (présence d’armes, d’éléments de chars et de vaisselle liée à la prise de boisson) et l’absence d’autres outils spécialisés. En revanche, la proportion de découvertes de poids et de balance est inversée entre les deux régions, les sépultures égéennes contenant plus souvent des balances alors que celles-ci sont rares en Europe159.
C. Pare adopte l’approche statistique développée par David George Kendall, pour analyser les données métrologiques des poids de balance du Bronze Final (voir le chapitre “Les statistiques appliquées à la métrologie”, p. 86-88). Il laisse de côté un grand nombre d’artefacts dont il juge la masse peu fiable (corrosion, action du feu, etc.) et propose donc un test basé sur les 17 poids de balance restants160.
Bien qu’il estime que les données sur la pratique de la pesée antérieure à l’âge du Fer sont trop abondantes et trop complexes pour être traitées dans son seul article, il propose toutefois un premier modèle de l’adoption et du développement des systèmes pondéraux. Il date les premières traces claires d’une pesée de précision vers le milieu du IIe millénaire a.C. dans la zone des Terramare, bien que l’usage de la balance à bras égaux puisse être antérieure, comme le montrent des travaux antérieurs comme ceux de M. Lenerz-de Wilde161 et M. Primas162. Peu de temps après, une pratique de pesée se développe en Europe centrale. Les systèmes métrologiques utilisés dérivent alors selon lui de ceux du monde égéen (fig. 1-17) avec l’utilisation de l’unité d’environ 61 g mise en évidence par K. Petruso163, mais ils seraient basés sur des systèmes de comptage différents164.
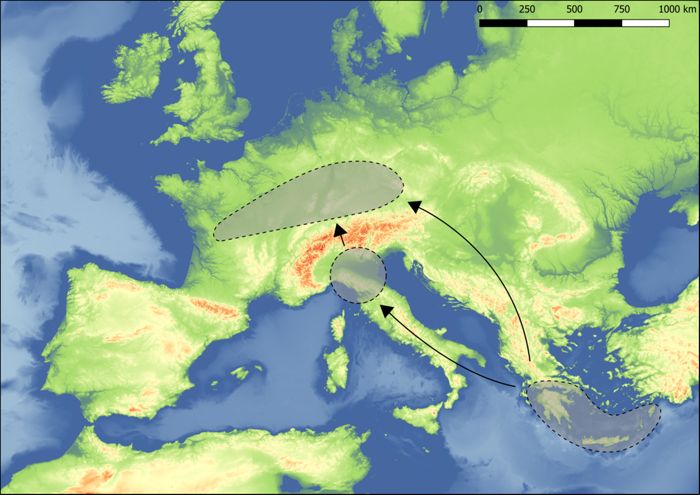
Pare 1999 et Pare 2013.
Enfin, C. Pare reste prudent dans son interprétation de l’usage pouvant être fait de ces systèmes de pesée. Il rappelle que les sépultures d’Europe centrale ne montrent pas d’indice de la spécialisation des individus enterrés (commerçant, métallurgiste, etc.) et que la pesée peut servir dans une grande variété de domaines du commerce ou de l’administration165.
Cette première synthèse des pratiques métrologiques livrée par C. Pare s’inscrit dans une logique diffusionniste qui véhicule l’idée d’une filiation directe ou indirecte entre la métrologie pondérale pratiquée dans l’Europe moyenne et celle en usage en Méditerranée orientale et centrale. Sa démarche se démarque cependant des courants purement comparatistes par son ancrage dans la documentation archéologique d’une aire géographique étendue. C. Pare propose un modèle cohérent de diffusion de proche en proche dont il identifie des jalons sur la base du matériel archéologique.
Son travail met aussi en lumière de manière irréfutable l’existence d’instruments de pesée en Europe centrale, dès l’âge du Bronze, et selon des modalités qui excluent la réception “passive” d’une technologie. Bien qu’il estime que l’unité pondérale utilisée soit la même que celle identifiée par K. Petruso dans le monde égéen, il met en avant l’utilisation en Europe de formes et de savoir-faire originaux dans la fabrication des instruments de pesée.
Le travail de C. Pare constitue un jalon essentiel dans les recherches sur la métrologie pondérale de l’Europe occidentale. Il présente une première catégorisation morphologique des poids du Bronze final, une analyse métrologique reposant uniquement sur les données archéologiques ainsi qu’un modèle interprétatif de l’usage des systèmes pondéraux. Ses résultats peuvent toutefois être aujourd’hui nuancés et complétés par les nouvelles découvertes et par une observation plus large des pratiques de métrologie pondérale à l’échelle de l’Europe occidentale.
Les fléaux de balance en os
du nord-ouest de la France
Bien qu’ils soient mentionnés par C. Pare, l’identification de fléaux de balance de l’âge du Bronze dans le Bassin parisien revient à un groupe de chercheurs basés en France dont les travaux sont publiés dans la même année 1999. C’est la découverte d’un objet en matière dure animale dans une sépulture à crémation du BF I-IIa sur le site de la “Croix de Mission” (Marolles-sur-Seine, Seine-et-Marne, France) et sa ressemblance avec un fléau de balance en alliage cuivreux identifié sur le site d’Hochdorf (Eberdingen, Bade-Wurtemberg, Allemagne) qui permet une première assimilation de ce type d’objet à un instrument de pesée. Sa présentation lors d’une journée d’actualité sur l’âge du Bronze organisée par la Société Préhistorique Française en 1999 (Toulouse) et la découverte d’objets similaires, peu de temps auparavant, dans la grotte des Perrats (Agris) et La Cave Chaude au Bois du Roc (Vilhonneur, Charente, France), permettent à R. Peake, J.-M. Séguier et J. Gomez de Soto d’écrire une courte synthèse sur ces artefacts166. Un deuxième article, un peu plus conséquent, est publié l’année suivante dans la revue Archéopages par deux signataires du premier167.
Ces objets, en os ou en bois de cerf, sont de petites dimensions (généralement moins de quinze centimètres) et renvoient à une pesée de précision. Leur découverte et leur identification ouvrent grandement vers l’Ouest la zone géographique où une pratique pondérale est connue pour l’âge du Bronze. Il est cependant encore difficile à la fin des années 1990 de déterminer le spectre d’utilisation de ces objets et leur possible corrélation avec des poids de balance.
Ces deux travaux mettent toutefois en évidence l’existence d’une activité de pesée, probablement dès la fin de l’âge du Bronze Moyen (d’après la datation de l’exemplaire d’Agris168) et vraisemblablement jusqu’à la fin du Bronze Final, archéologiquement illustrée par de petits fléaux de balance en matière dure animale (os ou bois de cervidé) retrouvés dans le sud-est du Bassin parisien et en Charente. De plus, dans le Bassin parisien, ces instruments sont retrouvés en contexte funéraire, dans des sépultures fondatrices ou d’individus de rang élevé169.
Les derniers travaux et bilan
En dehors des quelques études majeures abordées plus haut, les travaux consacrés aux poids de balance et à la métrologie demeurent réduits. Depuis le début des années 2000, nous comptons essentiellement quelques articles et des découvertes pour la plupart issues d’opérations de fouilles préventives.
Concernant la recherche fondamentale sur le sujet, il faut citer l’article publié en 2007170 par C. Pare, à qui l’on devait déjà l’étude sur les instruments de pesée de l’âge du Bronze en Europe centrale171, et Lorenz Rahmstorf qui s’est spécialisé au début des années 2000 dans la recherche des plus anciennes traces de la pratique de la pesée en Méditerranée centrale et nord orientale172. Les auteurs se sont penchés sur l’identification de poids de balance en pierre pour la fin du Premier âge du Fer et la période de La Tène. La majorité des poids de balance présentés correspondent à des exemplaires ovoïdes ou piriformes généralement pourvus d’une bélière en fer, dans la plupart des cas corrodée ou disparue173, semblables à ceux décrits par A. Cardarelli et alii dans les Terramare et la Suisse (fig. 1-18)174. Leur analyse métrologique semble bien montrer des convergences de masses autour de certaines valeurs (notamment autour de 300 g) pour lesquelles peuvent également être identifiés des multiples175, mais selon eux les écarts sont trop élevés pour restituer un système métrologique clair176.

Nous devons également à L. Rahmstorf un essai sur l’existence et l’identification de pebble weights, autrement dit l’utilisation opportuniste d’objets lithiques peu ou pas travaillés comme poids de balance177. L’hypothèse est théoriquement très intéressante car elle souligne le possible manque d’identification des poids en raison de leur simplicité morphologique. Malheureusement, son argumentaire repose sur un nombre réduit d’exemples : Bordjoš (Vojvodina, Serbie), la tombe 298 de la nécropole “Le Petit Moulin” (Migennes, Yonne, France) et la tombe 37 à Steinheim-Mülheim (Hesse, Allemagne)178. S’il n’est pas réellement possible de tirer de conclusions à propos des systèmes métrologiques utilisés dans la sélection et/ou la mise en forme de ces lots d’objets lithiques, leur standardisation pondérale semble cependant bien mise en évidence et amène à s’interroger sur l’existence d’autres ensembles de poids de balance en pierre n’ayant pas été identifiés jusqu’à présent179.
Plus récemment, L. Rahmstorf a dirigé un projet financé par l’European Research Council (ERC) et centré sur la métrologie pondérale de l’âge du Bronze entre Atlantique et Indus (Weight and Value). Ce projet d’envergure a remis la question de la métrologie au centre du débat archéologique et a amené un certain nombre de publications, notamment sur la métrologie pondérale de l’Europe occidentale à l’âge du Bronze180.
Parmi les découvertes incontournables des deux dernières décennies, il faut citer les “lots de peseurs” découverts dans des tombes du BF1 (v. 1275-1150 a.C.) à Migennes “Le Petit Moulin” et Étigny “Le Brassot” (Yonne, France). Les deux sites sont fouillés par l’Inrap respectivement en 2004 et 1999 mais passent relativement inaperçus pendant plusieurs années malgré le caractère inédit des découvertes en matière de pratique pondérale. En plus des rapports de fouilles181, le site de Migennes a fait l’objet d’une étude plus poussée dans le cadre du mémoire de Master de Mafalda Roscio182 puis d’un article paru en 2011183 et enfin d’une publication de thèse récente184. La caractéristique principale de ces deux sites est la présence conjointe de fléaux et de poids de balance, a priori rassemblés dans des coffrets en matières périssable faisant l’objet d’un dépôt funéraire. Ces deux découvertes mettent pour la première fois en évidence l’association de fléaux de balance en matière dure d’origine animale et de poids de balance en alliage cuivreux ainsi qu’une probable pratique de réutilisation opportuniste d’éléments métalliques (têtes d’épingle) comme poids de balance.
Pour résumer les avancées des trois dernières décennies marquent en Méditerranée et en Europe le passage d’une métrologie historique, fondée sur la comparaison avec un catalogue d’unités connues par des textes proche-orientaux, à une “métrologie archéologique” dans laquelle l’analyse des instruments de pesée est le centre de gravité. Les recherches sont inégales, certaines prennent racine plusieurs années plus tôt, mais le fait est que la majorité des travaux majeurs permettant cette transition sont publiés entre 1990 et 2000, tout du moins pour ce qui concerne l’Europe et la Méditerranée centrale et occidentale.
Entre la fin des années 1990 et le début des années 2000, le mobilier archéologique devient la donnée principale des études métrologiques. Les longues listes d’unités pondérales définies par les métrologues du début du XXe s., en particulier pour les populations de la Méditerranée orientale, sans tomber dans la désuétude, loin de là, sont prises avec le recul nécessaire. Des typologies morphologiques de poids de balance commencent à émerger, bien que de manière timide, il commence à être possible d’observer des différences morphologiques dans le temps et l’espace. Les formules mathématiques et les tests statistiques s’affirment également comme des outils incontournables des études sur la métrologie ancienne, et l’analyse quantale développée par D. G. Kendall185 s’installent comme une référence en la matière.
Même si la comparaison avec les systèmes pondéraux orientaux reste au centre de beaucoup de travaux, l’idée de l’existence de systèmes ou d’adaptations autochtones commence à faire son chemin. Enfin, de manière indépendante mais contemporaine, l’augmentation significative du nombre d’opérations archéologiques, la rigueur méthodologique atteinte en cette fin de siècle et l’amélioration des publications (qualité générale, facilitation de l’impression des planches de mobilier, démocratisation sensible de l’édition, etc.) participe grandement à l’accès à une donnée permettant l’identification d’instruments de pesée.
III. La péninsule Ibérique : un territoire à part ?
La péninsule Ibérique se distingue fortement du reste de l’Europe occidentale par l’intérêt accordé à la métrologie pondérale ibérique tout au long du XXe s. Le développement de ces recherches s’appuie sur une identification relativement précoce d’un type de poids de balance original et une approche comparatiste fortement tournée vers la Méditerranée centrale et orientale.
1. Isidro Ballester et les premières identifications
La première étude consacrée à des instruments de pesée antérieurs à la Période Romaine en péninsule Ibérique est impulsée par Isidro Ballester en 1930. Cet avocat de profession, spécialiste de l’archéologie ibérique et premier directeur du Museo de Prehistoria de Valencia, présente une communication sur le sujet lors du 4e Congreso Internacional de Arqueología, publié la même année186. Son travail va constituer un socle à l’étude la métrologie pondérale en péninsule Ibérique.
Son analyse repose sur la mise en évidence d’une série d’objets en alliage cuivreux et en plomb découverts lors des fouilles qu’il réalise à Covalta (Albaida, València, Espagne), dans les deux premières décennies du XXe s., et dont il observe des parallèles à València et Alacant187. Les objets en question se présentent généralement comme des troncs de cône en alliage cuivreux, de faible hauteur, de diverses tailles et percés en leur centre. Ils sont datés entre la fin du Ve et le début du IIIe s. a.C. (fig. 1-19). D’autres pièces, en plomb, possèdent des caractéristiques similaires, en particulier l’existence d’une perforation centrale, mais ils adoptent selon lui une forme plus cylindrique voire discoïde188. La fonction de ces objets échappe dans un premier temps aux fouilleurs, jusqu’à la fouille de la construcción 27 du departamento b en août 1918, où est mis au jour un lot complet de quatre d’entre eux, de dimensions distinctes. Ils paraissent abandonnés en position de rangement, empilés les uns sur les autres en ordre décroissant sur un axe en fer, lui-même rattaché à un disque en fer servant de base à l’ensemble (fig. 1-19)189.

Ce premier travail sur la métrologie pondérale de la période ibérique, bien que précurseur, est déjà très abouti. Il s’appuie sur un inventaire d’une cinquantaine de poids de balance provenant de plusieurs sites de la communauté autonome de València : Covalta, La Bastida de les Alcusses (Moixent, València, Espagne), El Cabeçó de Mariola (Alfafara-Bocairent, València, Espagne), La Serreta (Alcoi/ Concentaina/Penáguila, Alacant, Espagne) et El Xarpolar (Vall d’Alcalà, Alacant, Espagne). Dans son article, I. Ballester définit les grandes caractéristiques typologiques permettant l’identification des poids de balance du Levant Ibérique et, comme nous le verrons plus tard, de toute la péninsule : une forme générale cylindroïde (tronconique, cylindrique, discoïdale ou prismatique dans ses exemples), l’usage d’un métal fusible et une perforation centrale permettant l’insertion dans un dispositif de rangement.
Comme bon nombre d’analyses de poids de balance, passé les considérations morphologiques, typologiques et contextuelles, le cœur de son discours est centré sur un examen métrologique. Sur ce point, son travail présente plusieurs qualités non négligeables, la principale étant l’observation et la pesée directes qu’il fait du mobilier. Cela lui permet notamment d’exclure les objets qu’il estime trop oxydés pour connaître leur masse originelle190. Il identifie également des pratiques d’ajustement pondéral caractérisé par l’ajout de bagues ou de fils métalliques ou par l’évidement partiel des bases des objets (fig. 1-20)191. D’un point de vue méthodologique, il observe sept valeurs autour desquelles semblent se concentrer les masses de la plupart des poids de balance étudiés. Cela lui permet de procéder à un classement de 32 poids selon des valeurs centrales nommées de A à G dont il donne la moyenne ainsi que la différence absolue entre les valeurs minimale et maximale du groupe (fig. 1-21)192. Sur les 39 poids classés par I. Ballester selon ce système, seuls sept ne paraissent pas s’y intégrer. Il remarque que les cinq premières valeurs présentent des relations arithmétiques nettes, bien qu’il observe certaines erreurs et déviations, de telle manière que les valeurs A, B, C, D et E entretiennent un ratio de 10 : 6 : 4 : 2 : 1. La valeur F, quant à elle, est le double de la valeur g. Le rapport entre E, F et g, indique selon l’auteur l’existence d’une unité pondérale avoisinant les 4 g, qui correspond alors à la moitié de G mais également à la différence entre E et F et permet la création d’un système avec les multiples avoisinant les valeurs 8, 12, 16 et 20 g193.

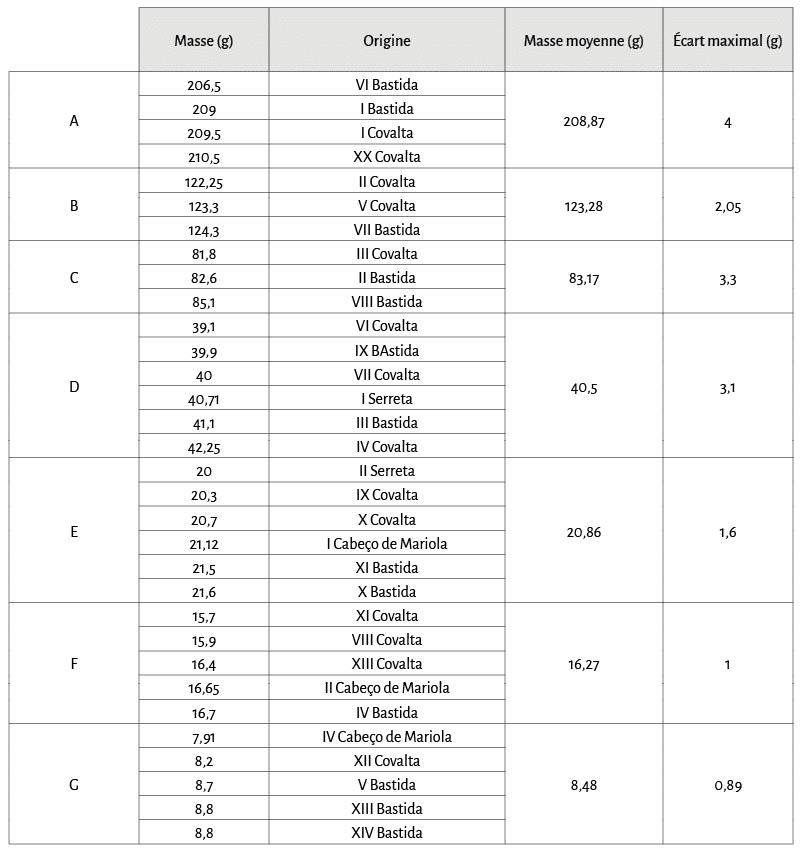
L’observation répétée de masses significativement similaires pour des objets de même forme amène Isidro Ballester à conclure qu’il existe bel et bien une pratique de la pesée et un système métrologique dont le développement reste cependant à caractériser mais qui est en usage au moins à la fin du IIIe s. a.C. et dans certains cas plus tardivement194. Il est intéressant de noter que si I. Ballester donne dès cette première publication une base analytique importante et un cadre méthodologique somme toute cohérent, il ne s’aventure pas à proposer une interprétation de l’origine d’un tel système pondéral.
2. Une démarche qui fait école
Dans ses grandes lignes, le travail initié par Isidro Ballester en 1930 va “faire école” ou en tout cas servir de terreau au développement des approches métrologiques du XXe s. en péninsule Ibérique. Les recherches sur la métrologie pondérale en péninsule Ibérique ne vont pas connaître un engouement semblable à ce que l’on peut observer au Proche-Orient. En revanche, les critères d’identification mis en évidence par I. Ballester vont permettre une mise à jour régulière des données archéologiques et une certaine évolution des modèles interprétatifs.
Pío Beltrán et la “mine covaltine”
En 1948, Pío Beltrán, docteur en mathématiques et numismate fortement reconnu dans l’archéologie ibérique valencienne, est le premier à rouvrir le dossier des poids de balance ibériques195. Son travail s’appuie globalement sur les données exposées par I. Ballester quelques années plus tôt bien qu’il mentionne la découverte de nouveaux poids dans la région196. À la différence de son prédécesseur, son approche est fortement teintée par l’école comparatiste de la deuxième moitié du XIXe s. et en particulier par les travaux de C. F. Lehmann Haupt. Ce dernier s’inscrit pleinement dans la tradition de la métrologie historique comparative décrite plus haut qui consiste à chercher les unités pondérales occidentales dans les listes de shekels et mines dressées pour la Méditerranée orientale. L’une des caractéristiques du courant dans lequel s’inscrit C. F. Lehmann Haupt est de réfuter l’idée de Normzone et d’attribuer donc à chaque variation métrologique observée sur les poids une tendance locale ou temporelle197. P. Beltrán s’appuie notamment sur la révision que fait ce dernier de l’article de I. Ballester en 1931 dans lequel il rapproche l’unité A (d’environ 208,9 g) de la moitié d’une mine d’or babylonienne légère de 421 g correspondant à un shekel de 8,4 g rapproché quant à lui de l’unité g.
Dans son article, P. Beltrán ne s’attache pas tant à vérifier la véracité de l’origine proche-orientale du système utilisé en péninsule Ibérique, origine qui semble admise pour lui, qu’à en chercher l’identification exacte. La tradition explicative n’est pas propre à la question de la métrologie, bien qu’elle aura peut-être une postérité plus longue dans ce domaine, mais à la tendance générale de la définition des cultures matérielles de la péninsule Ibérique en fonction de critères propres aux contacts et apports de populations venues de Méditerranée (Phéniciens puis Grecs).
Son travail se focalise ainsi sur la définition de ce qu’il nomme la “mine covaltine”, qu’il déduit du site éponyme de Covalta. Son argumentation repose sur l’analyse du lot de poids de balance trouvé dans la construcción 27 du departamento b, sur lequel reposait déjà l’identification d’I. Ballester. Selon lui, ce lot est construit autour d’une unité d’environ 41 g, représentée par le poids le plus léger, ainsi que son double, son triple et son quintuple, permettant l’obtention du ratio 1 : 2 : 3 : 5. Cependant, le fait que la somme totale des poids soit égale à 11 fois l’unité (1 + 2 + 3 + 5) lui semble incongru. Il déclare en effet que les “anciens utilisent les systèmes décimal et duodécimal mais pas la base onze”. Par conséquent, il juge que le lot est en réalité complété par le dispositif en fer qui permet leur rangement. Celui-ci, toujours selon P. Beltrán, pèserait la masse de l’unité, soit environ 41 g, et permettrait donc l’obtention d’un lot complet, constitué des poids 1 : 1 : 2 : 3 : 5, égal donc à douze fois ladite unité (1 + 1 + 2 + 3 + 5) mais également à la fameuse mine covaltine soit 497,1818 g selon l’auteur. Il renforce son argumentaire en comparant la construction ainsi obtenue avec la suite de Fibonacci198. Cette célèbre suite arithmétique est formée de nombres entiers dont chaque terme est la somme des deux précédents. Elle est généralement commencée par les termes 0 et 1, donnant ainsi :
{0, 1, 1, 2, 3, 5, 8, 13…}
P. Beltrán s’attarde ensuite à proposer diverses hypothèses concernant l’origine de cette mine qui pourrait être soit une mauvaise copie de la mine réelle babylonienne légère de 504-505 g, soit de la mine réelle utilisée par les Perses, avoisinant les 500 g. Sa dernière hypothèse est qu’elle soit importée par les Carthaginois qui utilisent une drachme de 3,74 g dont les 4/3 valent 4,9872 g qui, multipliés par 100, équivalent à 498,72 g, soit une valeur très proche de celle qu’il définit pour la “mine covaltine”199.
Un tel raisonnement méthodologique peut amener à trouver des parallèles entre toutes les unités ayant un jour été utilisées de par le monde et nous ne pouvons donc pas le considérer comme scientifiquement satisfaisant. Cependant, on remarque que P. Beltrán considère dès 1948 comme admis que le système pondéral en usage en péninsule Ibérique à l’âge du Fer est d’origine exogène. Ce postulat est d’une importance capitale pour l’étude de la métrologie ibérique car il ne sera quasiment jamais remis en question par la suite.
L’école comparatiste en péninsule Ibérique
Dans la suite de P. Beltrán, plusieurs auteurs espagnols adoptent un modèle d’analyse foncièrement diffusionniste et appuyé à une approche comparative. En 1964, Emeterio Cuadrado Díaz, un ingénieur de profession grandement impliqué dans l’archéologie ibérique, publie la découverte de deux lots importants de poids de balance, ceux de la tombe 200 d’El Cigarralejo (Mula, Murcia, Espagne) et de la tombe 117 de Cabecico del Tesoro (Verdolay, Murcia, Espagne), et reprend le dossier de la métrologie ibérique200. Les deux lots présentés sont d’un grand intérêt en raison du nombre élevé de poids qui les composent, de leur découverte dans des contextes clos et d’une datation de la fin du Ve ou début du IVe s. a.C. plus ancienne que celle des exemplaires de Covalta.
Méthodologiquement, son travail repose essentiellement sur une comparaison entre les valeurs des poids présentés et les systèmes connus en Méditerranée. E. Cuadrado estime probable que le système pondéral ibérique soit adapté de celui utilisé par les Grecs au VIe s. a.C., fondé sur une drachme de 4,36 g et une mine de 436,6 g201. Il admet toutefois qu’il est difficile de définir catégoriquement quel système pondéral inspire celui des Ibères puisque les systèmes grecs, babyloniens, phéniciens et d’Asie Mineure sont reliés aux mêmes patrons et diffèrent surtout par leurs diviseurs202.
Par la suite, la découverte régulière de poids de balance sur les sites ibériques et l’étoffement du corpus qui en résulte amène à la production de plusieurs articles au cours des années 1980 et 1990. En 1981 Domingo Fletcher Valls et Consuelo Mata Parreño publient une étude aspirant à être exhaustive203. La méthode employée se veut innovante, notamment en raison de l’effort de classement des poids selon leur chronologie lorsque cela est possible. Toutefois, elle repose sur l’hypothèse de l’origine grecque du système pondéral ibérique, déjà émise par E. Cuadrado204. La confirmation de leur hypothèse passe par une analyse arithmétique qui consiste à diviser la masse de chaque poids étudié par l’unité théorique qu’ils souhaitent mettre en évidence, à savoir la drachme de 4,36 g. Le quotient ainsi obtenu permet de déterminer à quels diviseurs ou quels multiples de la drachme correspondent les poids ibériques205. Les auteurs concluent qu’au IVe s. et au début du IIIe s. a.C., les Ibères utilisent un système pondéral “directement lié aux usages des Grecs”206. Cependant, la démonstration fait fi des déviations entre masses réelles et théoriques qui atteignent parfois des valeurs particulièrement élevées, surtout dans les valeurs les plus basses, et donc les plus proches de la drachme elle-même (jusqu’à 27,6 % de déviation relative pour un poids de 3,7 g assimilé à un tétrobole de 2,9 g).
J. Pellicer i Bru propose peu de temps après un court article sur la métrologie ibérique en s’appuyant abondamment sur les comparaisons avec les unités monétaires locales ou non. Il conclut sur l’utilisation d’un poids monétaire autochtone de 408 g, dérivé d’un patron phocéen, auquel correspond une unité de 4,08 g qui se retrouverait dans les poids de balance ibériques207.
En 1995, D. Fletcher publie un nouvel article sur le sujet accompagné par Luciano Silgo Gauche. Les auteurs y listent les découvertes faites sur le sujet depuis 1981 sans questionner l’hypothèse alors acquise de l’origine méditerranéenne de la métrologie ibérique. Les conclusions vont toutefois plus loin en proposant l’usage d’une mine d’origine méditerranéenne, autour de 500 g, employée principalement dans le cadre de la pesée du métal à des fins prémonétaires208. Les auteurs introduisent également la présentation d’inscriptions a priori métrologiques dont celle du cuenco de la Granjuela, publié depuis alors quelques années209. Ce récipient en argent arbore une inscription, dont le caractère numéral est probable et qui, selon Francisco Javier Oroz Arizcuren, annoncerait la masse de métal utilisée pour le concevoir210.
Dans les années 1990, en péninsule Ibérique, le modèle d’étude métrologique comparative, initié par C. F. Lehmann Haupt et P. Beltrán, est déjà installé et semble bien ancré dans les esprits. L’idée communément admise est alors que le système pondéral en vigueur dans le Levant ibérique prend son modèle chez ceux des populations de Méditerranée centrale ou orientale dans le cadre des relations commerciales entretenues entre les deux zones. Ce dernier article est très certainement représentatif de l’enlisement de la recherche en métrologie ancienne de la péninsule Ibérique en cette fin de XXe s. et des écueils systématiques de la méthodologie employée.
La reconstitution de la mine, notamment, s’appuie sur l’idée de l’origine méditerranéenne du système et donc de l’existence de la “mine covaltine”, proposée par P. Beltrán un demi-siècle plus tôt211 sans être remise en question. Pourtant, bien que le corpus s’élève alors à plus de 130 artefacts, seul un poids de balance avoisine les fameux 500 g. Or, ce poids de 493,3 g, la fameuse mine, qui sert dans cet article à reconstruire le système métrologique212, n’est pas sans poser problème. Il est cité et décrit brièvement par I. Ballester213 puis identifié comme une possible mine (alourdie par un huitième de mine) par D. Fletcher et C. Mata214 avant qu’elle ne soit considérée comme la seule mine ibérique connue et qu’elle serve de base à une extrapolation métrologique en 1995215. Cependant, la révision du matériel effectuée dans le cadre du travail présenté ici a permis de déterminer que le poids décrit par I. Ballester en 1930 correspond à l’objet Bas-68-A de notre corpus, ne pesant pas 493,3 g mais 193,82 g. Il s’agit donc vraisemblablement d’une coquille faite par I. Ballester plusieurs décennies plus tôt et qui n’a jamais été relevée (l’objet a cependant probablement été repesé puisqu’un poids de 193,3 g est mentionné à La Bastida216 bien que l’association entre les deux n’ait jamais été faite). Ce constat permet de fortement remettre en question l’identification d’une “mine” en péninsule Ibérique et pointe l’éloignement progressif entre les modèles interprétatifs et la donnée archéologique.
En dehors des études focalisées sur les poids, un article est consacré pour la première fois en 1990 à la balance à deux plateaux dont l’existence n’est alors que suggérée en négatif par l’existence des poids217. Bien que court, ce travail mené par María Rosario Lucas Pellicer fait un inventaire succinct des différentes découvertes de fléaux et plateaux de balance, en péninsule Ibérique mais également à plus large échelle, en Angleterre et en Sicile. L’auteure propose également une reconstruction de ce que peuvent être les balances à bras égaux en péninsule Ibérique sur la base de l’information archéologique et les contraintes mécaniques de celles-ci218.
Grau Mira et Moratalla Jávega :
les poids de balance sous un jour nouveau
Au début des années 2000, Ignacio Grau Mira et Jesús Moratalla Jávega proposent une profonde relecture des poids retrouvés dans le Levant ibérique et étudiés tout au long du XXe s.219. Cette publication s’inscrit dans une problématique d’étude de la gestion d’un territoire qu’ils restituent comme la “Contestania Ibérica” et plus particulièrement de la régulation des mesures pondérales à partir d’un important corpus composé de plus de 160 poids de balance. En plus d’une brève interrogation sur les éléments pouvant influencer l’étude métrologique (tolérance pondérale ancienne, erreurs non intentionnelles, variations géographiques et chronologiques, état de conservation et erreurs de mesure modernes220) et une présentation des pièces inédites, les auteurs s’attardent sur des composantes souvent ignorées dans les études antérieures. Pour la première fois, une place est laissée aux caractéristiques morphologiques des poids221, aux marques que présentent certains d’entre eux222 ainsi qu’aux traces de transformations de certains223, déjà observées par I. Ballester224 mais restées en marge depuis.
D’un point de vue méthodologique, ils reprennent le regroupement par valeurs similaires en séries proposé par I. Ballester225 puis repris par D. Fletcher et L. Silgo226. Les auteurs reprennent les valeurs moyennes publiées par I. Ballester, et D. Fletcher et L. Silgo, qu’ils recalculent en y incluant les données inédites227. Ainsi, si cette étude n’intègre pas les procédés statistiques employés par ailleurs depuis plusieurs années, elle reprend en revanche les traits les plus intéressants des études antérieures sur la métrologie ibérique, notamment l’extrapolation de valeurs principales autour desquelles les masses convergent pour en déduire des systèmes de comptage et des unités. À travers cette méthode, les auteurs en arrivent notamment à distinguer plusieurs systèmes métrologiques distincts selon leur chronologie.
En résumé, ils identifient, sur la base de leur analyse, l’utilisation d’un système construit autour d’un standard de 8,6 g au IVe s. a.C. et qui dériverait d’une double drachme athénienne de 4,36 g. Il serait alors utilisé de manière privilégiée mais non exclusive. Au IIIe s., il perdurerait et coexisterait avec un autre construit autour d’une unité de 7,2 g. Enfin, aux IIe et Ier s. a.C., le standard de 8,6 g serait abandonné au profit d’un nouvel étalon d’environ 7 g228.
L’article d’I. Grau et J. Moratalla reste inscrit dans une tradition historiographique comparative et n’offre pas, en ce sens, de profonds changements. Cependant, les instruments de pesée y sont appréhendés sous un jour nouveau. Pour la première fois, la métrologie est replacée dans un monde mouvant dans le temps et dans l’espace et les systèmes restitués sont considérés selon des limites chronologiques, économiques et politiques permettant pour la première fois d’aborder réellement l’idée d’unités pondérales locales.
Le dossier a été plus récemment repris par nous-même dans le cadre d’une approche plus locale à partir de l’exemple du lot de dix poids découverts dans la tombe 200 d’El Cigarralejo229 publié et étudié cinquante plus tôt par E. Cuadrado230. Cet article propose une nouvelle lecture métrologique de ce lot en s’appuyant sur l’analyse des relations arithmétiques des différents éléments d’un lot entre eux (“tableau de division”) (voir le chapitre “Retrouver les relations arithmétiques”, p. 82-84). Nous y proposons l’identification d’une unité métrologique locale d’environ 20,7-20,8 g au centre de la constitution d’un lot de poids de balance complexe permettant la réalisation de tous les multiples de l’unité jusqu’à vingt-quatre fois celle-ci231. Si cette unité peut mathématiquement correspondre à trois fois l’unité de 7,2 g identifiée par I. Grau et J. Moratalla232, cette dernière ne semble toutefois pas pouvoir expliquer la construction arithmétique du lot lui-même en tant qu’outil fonctionnel.
Plus récemment, nous avons repris avec Lysiane Delanaye le sujet des modifications de poids de balance et de l’impact de celles-ci sur la masse des artefacts et leur utilisation233. Les résultats de cette étude sont en grande partie présentés plus loin (voir le chapitre “Fabriquer des instruments de pesée ‘ibériques’”, p. 304-308).
3. À l’Ouest, du nouveau
Alors que le Levant espagnol commence à être bien connu du point de vue de la métrologie pondérale, la fin des années 1990 et les années 2000 marquent la prise de conscience de l’existence de procédés similaires dans la moitié ouest de la péninsule Ibérique et de l’ancienneté de cette pratique. L’une des premières publications qui modifie réellement l’état de l’art est celle de la totalité des instruments de pesée découverts sur le site de Cancho Roano (Zalamea de la Serena, Badajoz, Espagne)234.
Le “palais-sanctuaire” de Cancho Roano
Par bien des aspects, le site de Cancho Roano et les instruments de pesée qui y sont trouvés, revêtent un caractère exceptionnel. Tout d’abord, le site correspond à un grand édifice en adobes et sous-bassement de pierres, daté du Ve s. a.C.et interprété par les fouilleurs comme un “palais-sanctuaire”235. En raison de cette interprétation, l’utilisation même des instruments de pesée est imaginée dans un contexte d’administration à caractère probablement religieux236 attesté par certains artefacts interprétés comme des objets votifs237. De plus, le site ayant été fouillé intégralement et méthodiquement, il est possible de contextualiser les découvertes à l’intérieur même de celui-ci, une donnée malheureusement souvent inaccessible dans la plupart des études antérieures de métrologie238. Un troisième point important est la présence de marques numérales sur la moitié des poids de balance découverts sur le site239. Cet élément est primordial car il permet plus que tout autre d’orienter la recherche d’unités métrologiques. Au moment de la publication de l’ensemble de poids de balance de Cancho Roano, aucune marque de ce type n’avait alors été clairement identifiée au sein du large corpus des poids ibériques. Du point de vue de la métrologie en usage, María Paz García-Bellido met dans un premier temps en évidence plusieurs systèmes pondéraux potentiels (fig. 1-22) d’après l’observation des masses et des marques numérales et s’interroge sur l’existence d’au moins deux systèmes différents240. Elle conclut toutefois à l’utilisation d’un seul système marqué par de fortes déviations et basé sur une unité de 9,4 g dont les meilleurs parallèles sont à chercher dans les poids phéniciens de la côte syrienne et datés de la fin du Ier millénaire a.C.241.
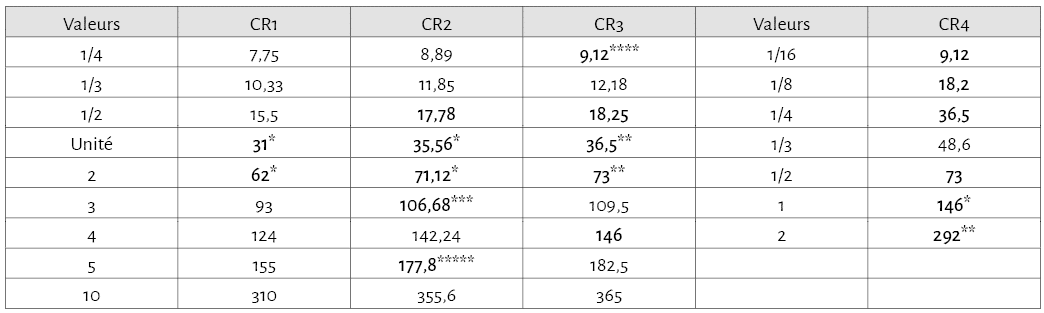
Cette interprétation s’inscrit clairement dans une tradition de métrologie comparative et de recherche de l’origine du système pondéral à l’extérieur de la péninsule Ibérique. M. P. García-Bellido voit dans l’utilisation du shekel ougaritique/syrien la marque du maintien des connexions avec l’Orient méditerranéen, alors même que son utilisation en Phénicie semble moins répandue à cette époque qu’au préalable242. La reconstruction métrologique de M. P. García-Bellido ne manque pas de cohérence mais se heurte toutefois à plusieurs écueils. Il faut mentionner que sur les 26 poids de balance retrouvés à Cancho Roano, un seul correspond directement au shekel en question, à savoir le poids CR-C de 9,14 g selon Joan Maluquer de Motes et María Paz García-Bellido243, aujourd’hui pesé à 8,23 g (probablement en raison d’un prélèvement pour analyse métallographique) et marqué de quatre points. L’existence d’une oscillation plus ou moins grande des masses autour d’une valeur théorique centrale, la Normzone, n’est pas une nouveauté. En revanche, le fait que la Normzone soit aussi élevée (environ 15 % de déviation relative entre les poids de 31 g et 36,5 g), sur un même site et au même moment, pose problème, qui plus est lorsque celui-ci est interprété comme un lieu à vocation cultuelle dont l’une des fonctions, selon M. P. García-Bellido, serait d’entreposer les poids de balance faisant office d’étalons. Un tel raisonnement revient à dire que les instruments de pesée maniés par ces populations ne permettent pas de percevoir ces différences de masses. Mais il est toutefois improbable que des poids de 62 g et 73 g aient pu être assimilés à une même valeur alors même que leur différence de masse (9 g) est supérieure au poids le plus léger de la série (7,75 g) et similaire au deuxième plus léger (9,12 g). M. P. García-Bellido n’hésite d’ailleurs pas à proposer que la dispersion de la masse durant les périodes anciennes puisse atteindre 20 %244, une estimation critiquée par I. Grau et J. Moratalla qui estiment qu’elle empêcherait toute distinction entre deux valeurs consécutives d’une séquence arithmétique245.
Le nord-ouest de la péninsule Ibérique
Les pratiques de pesée dans le nord-ouest de la péninsule Ibérique sont connues par une série de découvertes plus ou moins importantes. C’est notamment la mise au jour de poids de balance sur les sites de La Hoya (Guardia, Araba, Espagne)246, La Custodia (Viana, Navarra, Espagne)247 et Munoaundi (Azkoitia-Azpeitia, Gipuzkoa, Espagne)248 qui a permis d’accroitre l’échelle d’observation de la pratique pondérale en péninsule Ibérique. Fernando Galilea Martínez intègre ces découvertes dans une synthèse sur les instruments de pesée trouvés en péninsule Ibérique249. L’auteur propose une vision originale qui s’intéresse pour la première fois à la péninsule Ibérique comme un seul ensemble géographique qui possède la particularité de livrer un type de poids de balance inconnu ailleurs : les poids métalliques cylindroïdes avec perforation centrale. F. Galilea distingue ainsi trois zones géographiques fournissant trois systèmes métrologiques différents :
- l’aire ibérique, avec une unité avoisinant les 21 g et un système construit par les multiples 1 : 2 : 4 : 6 : 10 et les fractions 1/10 : 2/10 : 4/10 et 8/10 ;
- l’aire tartessienne avec des unités de 31 g, 36 g et 146 g, organisées autour des multiples 1 : 2 : 3 : 5 : 10 ;
- l’aire celtibérique qui utilise un standard de 15,3 g et un système quinaire (base 5) pour les multiples 1 : 2 : 3 : 5 et duodécimal pour les fractions entre 1/12 et 12/12250.
Sa méthode de détermination des unités est très proche de l’observation arithmétique publiée ailleurs pour les poids d’El Cigarralejo251. En dehors des cas ou une marque est susceptible d’identifier l’unité d’un lot, il est nécessaire de rechercher des multiples exacts à cette unité dans les ensembles. Il estime qu’en prenant l’unité la plus basse des séries, les multiples obtenus s’avèrent incohérents dans le cas où des fractions sont utilisées252. En ce qui concerne l’utilisation de ces objets, F. Galilea y voit un fonctionnement d’ordre commercial, et plus particulièrement destiné à la pesée d’un métal servant de medium de paiement, bien qu’il ne précise pas s’il parle d’or, d’argent ou d’un autre métal253.
Raquel Vilaça : la découverte d’une pratique pondérale
de l’âge du Bronze
L’utilisation d’instruments de pesée dès l’âge du Bronze dans le sud-ouest de la péninsule Ibérique n’est connue que par les travaux entamés depuis le début des années 2000 par Raquel Vilaça254. Bien qu’il s’agisse d’une des contributions les plus récentes à l’historiographie de la pratique pondérale, elle traite d’une période chronologiquement antérieure. R. Vilaça a mis en évidence et étudié environ quatre-vingts poids de balance datés du Bronze final et du Premier âge du Fer provenant de deux zones qu’elle distingue : le Beira Interio et l’Estremadura255. Le premier impact significatif de ses résultats est qu’ils amènent à nuancer fortement l’hypothèse de l’origine grecque du système métrologique ibérique défendue depuis E. Cuadrado256. En effet, à la lumière des découvertes de R. Vilaça, il devient clair que la pratique pondérale préexiste de plusieurs siècles la période d’échanges intensifs entre la péninsule et la Grèce.
Du point de vue de la morphologie, R. Vilaça distingue cinq types de poids principaux qui sont utilisés au Bronze final : les discoïdes, les bitronconiques, les sphériques, les cubiques et les octaèdres (fig. 1-23). Contrairement à ce que C. Pulak a pu mettre en évidence dans les épaves d’Uluburun et du Cap Gelidonya, où chaque catégorie de poids de balance semble correspondre à un usage métrologique particulier257, il ne semble pas y avoir ici de lien entre la forme et la fonction des objets et certains lots présentent des poids de morphologies distinctes258. Les plus fréquents sont les discoïdes et les bitronconiques qui sont perforés en leur centre. Cette forme semble être celle qui se généralise à l’âge du Fer dans toute la péninsule Ibérique et pourrait, selon R. Vilaça, être l’héritage d’une tradition autochtone259. À l’inverse, les poids cubiques semblent être typiques des sites phéniciens du littoral (Cerro del Villar ou La Fonteta) entre les VIIIe et VIe s. a.C.260.

R. Vilaça propose le modèle d’une économie autochtone fonctionnant sur le principe du troc et maniant des concepts de pesée, plus ou moins développés, sur laquelle viendrait se développer la pratique pondérale qu’elle observe archéologiquement261. Les communautés indigènes auraient ainsi intégré comme unité fondatrice le shekel syrien/ougaritique de 9,4 g utilisé de manière extensive en Méditerranée dans la deuxième moitié du IIe millénaire a.C. Cette assimilation métrologique se ferait donc par commodité, pour faciliter des échanges dans un premier temps et se maintiendrait par la suite en péninsule Ibérique alors que le shekel hittite de 11,75 g est a priori préféré à celui de 9,4 g à partir de la chute du monde mycénien avant d’être lui-même supplanté par le shekel phénicien de 7,9 g262. Les poids de l’Occident péninsulaire, dont les masses sont comprises entre 1,82 et 37 g, serviraient à peser des matières légères et précieuses comme l’or, l’ivoire ou l’ambre263.
Les interprétations de R. Vilaça à propos de l’ouest péninsulaire intègrent pour la première fois l’idée d’une confrontation entre des pratiques métrologiques indigènes et des unités allogènes. Ces dernières seraient adoptées par commodité par les communautés autochtone, afin de faciliter des processus déjà existants, et non pas imposés ou importés en raison de l’absence d’une pratique initiale.
Très récemment, la publication monographique des poids découverts à Azougada (Moura, Alentejo, Portugal) a prouvé que les poids de balance discoïdaux et bitronconiques perforés continuent à être utilisés à l’ouest de la péninsule Ibérique au Ve s. a.C.264. L’auteure publie des poids inédits découverts lors des fouilles menées sur le site dans les années 1940 et 1950. L’étude est de qualité, malgré l’ancienneté des données et le manque de contexte stratigraphique, et l’ensemble rappelle fortement celui de Cancho Roano avec des poids de balance en alliage cuivreux bitronconiques portant des marques numérales associés à des poids discoïdes en plomb265. Du point de vue de la métrologie, l’auteure identifie deux unités : un shekel de 9,4 g qui découlerait de l’usage qui en est fait au Bronze final et un shekel de 7,83 g qui remonterait, quant à lui, aux contacts avec le littoral durant la transition vers la période orientalisante (VIIIe s. a.C.)266.
Les spécificités de la pratique pondérale
La pesée métrologique se démarque de beaucoup d’autres pratiques par le nombre de prérequis abstraits qu’elle implique. Il est ici question de présenter ces différentes spécificités afin d’aborder l’étude de la pratique pondérale de la manière la plus objective et scientifique possible.
I. Compter et mesurer :
un processus cognitif complexe
La capacité à compter et mesurer est un processus complexe souvent mis en relation avec celle d’écrire267 qui permet de rationnaliser et d’abstractiser un certain nombre de caractéristiques du monde. Cette abstraction passe par l’adoption d’un ensemble de conventions qui permettent de transformer l’analogique en numérique. La mesure, quant à elle, est la deuxième strate d’abstraction qui vient se déposer sur la pratique du comptage. Ainsi, le fait de compter et mesurer n’a rien d’anodin, il s’agit d’un processus profondément ancré dans les pratiques sociales et difficile à modifier.
1. Du nombre à la mesure
Alain Testart rappelle dans sa préface de Poids et Mesures en Asie du Sud-Est que les chiffres sont dans notre société actuelle une composante incontournable, un filtre au travers duquel passe toute l’information, qu’elle soit économique, politique ou sociale268. Ce processus d’abstraction par les chiffres est cependant une pratique récente, tout du moins dans son universalisme. En effet, on peut observer aujourd’hui la place primordiale qu’occupent les chiffres dans la transmission de l’information : finances, opinion publique, performances sportives, évaluation scientifique…
Comment aborder alors objectivement la notion de métrologie lorsque l’on traite de populations n’ayant pas laissé de sources écrites intelligibles ? Il semble nécessaire de revenir, au moins de manière générale, sur l’utilisation des nombres, de l’arithmétique et de la mesure comme procédés d’observation avant de pouvoir réellement traiter de leur incarnation archéologique.
Écriture et comptage :
deux procédés en corrélation ?
L’écriture et le comptage partagent un certain nombre de traits communs liés à une rationalisation et une abstraction du monde, amenant à l’organiser et à le hiérarchiser269. Ainsi, les deux procédés sont souvent associés et mis en avant comme des outils d’enregistrement améliorant le fonctionnement des premiers systèmes administrés270. Comme beaucoup d’autres procédés aujourd’hui totalement imbriqués et indissociables de notre quotidien, ils ont tendance à être perçus comme l’une des étapes indispensables d’un processus d’évolution linéaire. Pourtant, comme l’a parfaitement mis en évidence Susan Sherrat, l’écriture n’est pas un progrès technologique universel et que chacun adopte lorsqu’il est confronté à son existence, mais bien au contraire une technologie spécifique qui ne trouve d’intérêt que dans un certain contexte social271. Un tel constat est entièrement applicable à la numération qui vient répondre à un besoin de dénombrer dans certaines quantités et dans certains contextes uniquement. Celle-ci peut donc prendre autant de formes qu’il existe de besoins différents.
L’une des formes les plus connues de numération est l’usage de procédés mnémotechniques permettant de tenir des comptes. C’est notamment le cas en Mésopotamie, par l’utilisation de jetons (tokens), un phénomène bien mis en évidence par Denise Schmandt-Besserat et dont l’évolution et la complexification amènent au développement de l’écriture cunéiforme272. Cependant, il ne s’agit pas là d’un schéma évolutif universel. Le procédé de comptage conduit ainsi à grouper l’information, à la réduire à une unité minimale indivisible multipliable autant de fois que possible. Elle indique ainsi une forme d’abstraction qui ne va pas de soi, qui n’est pas innée, car tout n’est pas comptabilisable au premier coup d’œil. Ainsi, passé un certain nombre, qui ne sera certes pas le même pour tout le monde, un outil de compte devient nécessaire, peu importe que ce nombre soit de plusieurs milliers ou de quelques unités. Cependant, il est légitime de se demander si tous les contextes amènent à dépasser ce nombre. Même dans le cas contraire, il est probable que la vocalisation, la représentation mentale, passe par une certaine formalisation, matérielle ou non. La plus évidente, par laquelle nous sommes tous passés, et à laquelle certains continuent à avoir recours, est de “compter sur les doigts”. Les guillemets sont de rigueur car les doigts ne sont pas l’unique médium corporel permettant de formaliser l’information numérale.
Les bases de comptage ou systèmes numéraux
En effet, nous utilisons nos doigts pour compter car nous utilisons aujourd’hui majoritairement une base de comptage dite décimale. Ou bien est-ce justement parce que nous comptons sur nos doigts que notre système est devenu décimal ? Bien entendu, l’un et l’autre sont indissociables. Les systèmes de comptage se sont partout et de tout temps appuyés à des repères visuels.
Cependant, lorsque L. Rahmstorf conclut son article The concept of weighing en stipulant que les multiples d’un système de comptage se doivent d’être intuitivement compréhensibles pour être utilisables et donc correspondre aux systèmes décimaux (“2, 3, 4, 5, 10”), duodécimaux (“12”) ou sexagésimal (“60”) ou dérivés de ceux-là, il commet probablement une erreur273. En effet, cette conception découle directement de la vision moderno-centrée d’un monde gouverné par le système décimal et de ses propres confrontations avec les systèmes duodécimal et sexagésimal dans l’étude de la Méditerranée orientale de l’âge du Bronze.
En réalité, il y a probablement au moins autant de systèmes de comptage différents que de façons de catégoriser et de hiérarchiser le monde. Sans chercher aucunement l’exhaustivité, il est possible de de mieux comprendre ce que peut être un système numéral “intuitivement compréhensible” au travers de quelques exemples tirés de l’anthropologie ou de réminiscences dans des systèmes encore utilisés.
L’anthropologue Zdeněk Salzmann, de la Northern Arizona University, s’est intéressé aux modèles de construction des systèmes numéraux. Son étude l’a amené à différencier trois schémas principaux de constitution de ces systèmes : frame pattern, cyclique ou opératif. Le frame pattern est une succession de plusieurs morphèmes (ou unités linguistiques)274. En français, leur nombre est finalement assez réduit, les premiers morphèmes vont de un à seize, on trouve ensuite vingt, trente, quarante, cinquante, soixante, cent, mille, million, milliard etc. Tous les nombres intermédiaires sont formés par l’accolement de deux ou plusieurs morphèmes. Par exemple, le nombre 21 est créé par l’association des morphèmes “vingt” et “un”, chacun porteur d’un sens numérique.
Le schéma cyclique renvoie à une construction du système numéral qui catégorise une succession de morphèmes comme une unité réplicable pour construire le système275. Dans le cas du système décimal, le groupe en question serait de dix morphèmes, le cycle reprenant au 11e puis au 21e etc. Un grand nombre de systèmes sont définis ainsi : quinaire (base 5), décimal (base 10), duodécimal (base 12), vigésimal (base 20) ou encore sexagésimal (base 60). Cependant, en français les premiers morphèmes vont jusqu’à 16 (seize) et non jusqu’à 10. Dans un cycle décimal parfait, notre onze deviendrait dix-et-un, notre douze dix-et-deux etc. De plus, nos nombres portent également la trace d’un cycle vigésimal (soixante-dix, quatre-vingts, quatre-vingt-dix etc.)276. Salzmann observe cela, notamment chez les populations amérindiennes, et parle alors d’inconsistance de ces cycles au sein d’un système277.
Il propose pour cette raison un troisième schéma, dit opératif, qui par combinaison des deux premiers, puis par addition, soustraction et multiplication, permet le rendu des systèmes numéraux278. Pour reprendre l’exemple du système décimal dans la langue française, le nombre 90 est construit à l’aide de trois morphèmes (“quatre”, “vingt” et “dix”) et doit se comprendre comme le résultat de l’opération arithmétique : 4 x 20 + 10. Le “nonante” belge est quant à lui une transcription plus directe du cycle décimal. Selon Salzmann, l’emploi d’un système cyclique implique obligatoirement celle d’un système opératif279.
Certains des exemples les plus fascinants sur le sujet nous viennent de Papouasie Nouvelle-Guinée, ou en plus d’observer des systèmes numéraux atypiques, il est possible de remarquer leur variété sur une échelle géographique relativement réduite. Ainsi, le système de comptage Oksapmin possède une base 27, correspondant à 27 parties du corps qui sont nommées en effectuant l’opération, depuis le pouce droit jusqu’à l’auriculaire gauche280 (fig. 1-24). Pour compter des valeurs supérieures, ils continuent en formant une boucle et reprennent au poignet (n° 28) puis à l’avant-bras (n° 29), ce qui implique qu’en revenant au point de départ, la valeur obtenue n’est pas de 27 x 2 = 54 mais seulement de 49 (les cinq doigts de la main gauche n’étant pas recomptés sur le retour). Plus proche d’une énumération que d’un véritable comptage, les systèmes numéraux “corporels” ne sont pas destinés à compter de grands nombres, ceux des langages Awyu allant par exemple jusqu’à 23 en Kombai et en Mandobo, 38 en Korowai et 41 en Wambon281. La principale raison à cela est que ces différents systèmes ne sont pas cycliques282 car ils n’ont de sens que dans la sphère du langage corporel et ne peuvent pas en être détachés. Chaque nombre est nommé en fonction d’une partie du corps et non pas en fonction de la valeur numérale qu’il contient. Ainsi, bien que seul un frame pattern soit utilisé dans ces exemples, ils illustrent pourtant clairement que si la base de comptage décimale nous parait intuitive car nous possédons dix doigts, beaucoup d’autres possibilités existent.
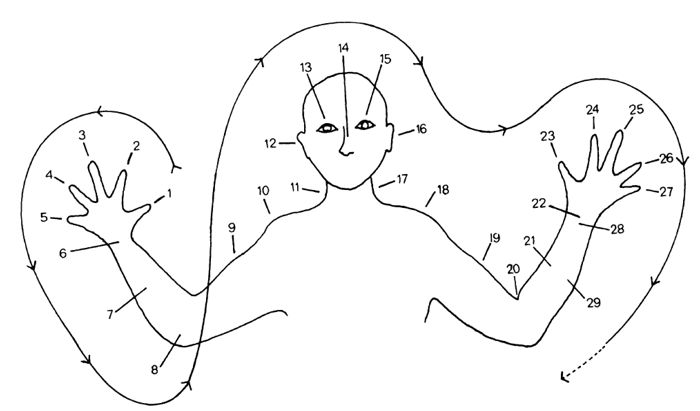
Ainsi, plusieurs sources témoignent de l’emploi de diverses bases numérales à travers le monde. On trouve plusieurs sociétés ou groupes humains utilisant un système vigésimal (base 20) dont le cycle contient parfois également un système quinaire tels que les Mayas283, ou décimal comme chez les Basques (fig. 1-25).
Le système sexagésimal (base 60) a été l’un des premiers utilisés, notamment dans la métrologie pondérale depuis le IIIe millénaire a.C.284. S’il ne parait pas évident au premier abord, il présente en réalité de nombreux avantages. Tout d’abord, il possède de nombreux diviseurs entiers (1, 2, 3, 4, 5, 6, 10, 12, 15, 20 et 30) ce qui facilite le calcul des fractions et 60 est également le plus petit nombre divisible à la fois par 1, 2, 3, 4 et 5. Ce système numéral est encore celui utilisé aujourd’hui pour calculer le temps (minutes et secondes), les angles (en degrés, minutes et secondes) ainsi que certaines coordonnées géographiques (également en degrés, minutes et secondes)285.
Enfin, bien que le système décimal se soit largement imposé, de nombreuses langues gardent des vestiges de systèmes numéraux aux structures différentes. En français, les structures quatre-vingts (4 x 20), quatre-vingt-dix (4 x 20 + 10) sont les réminiscences d’un système vigésimal, possiblement gaulois286 (bien que cette origine repose sur peu d’éléments), qui a en revanche en partie disparu en Suisse et en Belgique (huitante, uniquement en Suisse, et nonante). En anglais, eleven et twelve, comme les elf et zwölf allemands, sont quant à eux les dernières traces d’un système duodécimal. En danois, comme en français, un ancien système vigésimal est perceptible à travers des constructions qui nous paraissent aujourd’hui étonnantes, en particulier pour leur utilisation des fractions : 50 se dit halvtreds pour halvtredje-sinds-tyve qui peut s’entendre comme “deux vingtaines et la moitié de la troisième” soit 2,5 x 20 = 50. Ainsi, les nombres 60, 70, 80 et 90 sont exprimés en vingtaines et moitiés de vingtaines.
Il est ainsi très clair que vouloir réduire les systèmes de comptage à notre vision moderne et faussement décimale est loin d’être pertinent lorsque l’on observe des sociétés pour lesquelles on ne possède pas de témoignage écrit. Ainsi, un système se doit effectivement d’être intuitivement compréhensible mais nous nous fourvoyons en pensant que ce qui ne l’est pas pour nous ne pouvait pas l’être pour les populations anciennes. De plus, par le nombre de vestiges de systèmes anciens dans les langues parlées aujourd’hui, il est possible d’observer à quel point la numération est un facteur fortement ancré culturellement. Ainsi, les multiples et fractions qui ont du sens pour les uns sont parfois particulièrement ardus à appréhender pour d’autres.
Mesurer n’est pas compter
Cependant, la mesure implique l’acceptation d’une autre abstraction : l’unité métrologique. Ainsi, comme l’a dit Alain Testart, mesurer n’est pas compter287. La mesure, en premier lieu, ne nécessite pas de compter, elle a pour vocation de comparer. Cette comparaison se fait par rapport à une unité de référence dont la validité est circonscrite. Pour cette raison, la mesure est une convention288 qui possède ses limites et ne concerne donc jamais qu’une population. Combien d’unités métrologiques sont utilisées dans notre propre société sans pour autant concerner tout le groupe humain inclus dans celle-ci : le newton (poids), l’Ohm (résistance électrique), le bar (pression289) ?
La mesure peut s’appréhender de plusieurs façons, de la plus simple à la plus complexe. Elle peut être en effet purement intuitive et sensorielle et découler d’une simple perception des longueurs, des volumes et des masses. En effet, même dans notre société actuelle, de nombreux procédés de mesure ne passent pas par une comparaison directe à la norme en vigueur. Tous les jours, par exemple, et plusieurs fois par jours, chaque personne fait la mesure de la quantité de nourriture et d’eau nécessaire à sa survie avec une tolérance certes assez large. Mais combien de personnes mesurent réellement cette quantité avec les systèmes métrologiques adéquats ?
Dans d’autres cas, la mesure prend la forme d’une comparaison en fonction de standards plus précis mais pour autant bien éloignés de la précision généralement sous-entendue par le terme. Qui n’a jamais préparé un plat ou un dessert appelant des unités telles qu’une “cuillère à soupe” ou une “pincée” ? L’échelle de référence est intelligible, d’une portée suffisamment grande pour se permettre d’être publiée dans un ouvrage de cuisine, mais ne révèle pourtant d’aucune pratique de normalisation systémique.
Enfin vient la mesure telle que nous l’entendons généralement, celle s’appuyant sur des systèmes métrologiques définis, théorisés et largement acceptés. Et malgré leur large diffusion et démocratisation, ils ne sont appréhendés qu’avec des marges d’erreur très variables. En France, un produit vendu en supermarché selon une quantité donnée, doit correspondre à la mesure donnée selon une moyenne effectuée sur plusieurs produits. Celle-ci ne doit alors pas être inférieure à 99 % de celle annoncée pour les produits de plus de 15 000 g ou ml mais uniquement 91 % pour les produits de 5 à 50 g ou ml290.
Ainsi, la mesure et la numération sont deux processus distincts qui font appel à des concepts abstraits différents mais qui partagent une volonté d’organisation, de catégorisation et de hiérarchisation. Les deux notions sont cependant largement associées lorsqu’il s’agit d’organiser un système de référence selon une échelle donnée, autrement dit, lors du passage de l’unité au système métrologique.
2. De la mesure au système métrologique
Alain Testart différencie système numérique et système métrologique en argumentant que l’un sert à compter tandis que l’autre, dans sa vocation de mesure, se doit avant tout d’être facilement manipulable et notamment divisible291. Cela expliquerait bien l’usage du système sexagésimal en Méditerranée Orientale dès le IIIe millénaire a.C. En effet, la métrologie n’est pas uniquement le résultat du croisement entre unité et système numéral. Alors comment passer de la mesure au système métrologique ?
Multiples et diviseurs, entiers et fractions :
deux observations différentes du numéral
Un système métrologique peut se définir comme l’échelle de valeurs définissant les fractions et multiples d’une unité de référence. Son objectif premier est d’augmenter la capacité de comparaison d’un étalon de référence en offrant la possibilité de mesurer des éléments plus petits et plus grands que celui-ci. En effet, l’un des critères primordiaux d’un système métrologique est sa fonctionnalité, il n’a ainsi pas pour vocation de suivre avec exactitude un système numéral.
Les systèmes métrologiques se composent donc généralement de plusieurs unités reliées arithmétiquement entre elles ou de plusieurs valeurs, multiples et fractions, qui sans être nommées comme des unités à part entière, sont employées de manière relativement standardisée ou habituelle.
Ainsi, bien que le système métrique soit le système métrologique de référence pour les volumes en France, et que son unité soit le mètre cube, le litre (1 dm3) reste l’unité usuelle. Le système métrologique basé sur le litre suit le système décimal habituel avec des unités multiples (décalitre, hectolitre, kilolitre etc.) et des unités diviseurs (décilitre, centilitre, millilitre). Bien que ces unités ne soient pas intégrées au système international (SI) dont l’unité de capacité est le mètre cube, elles sont toutefois courantes dans de nombreux États et restent ainsi en usage et reconnues par ces derniers. Cependant, d’autres multiples ou fractions d’usages sont employés sans toujours être des unités à part entière. On peut noter par exemple 25 cl (le verre d’eau ou le demi de bière), 33 cl (la capacité habituelle des boites de sodas qui permet la plus grosse économie d’aluminium dans la réalisation du conteneur) ou encore 50 cl (la pinte française actuelle) mais également un grand nombre de conteneurs commerciaux destinés à la vente d’alcool292.
Les systèmes métrologiques se présentent donc comme des ensembles organiques, composés à la fois de normes établies par les entités politiques en place mais également des résultats des pratiques usuelles, de la tradition et d’autres habitudes sociales et économiques. Cette variabilité fait que les systèmes métrologiques peuvent parfois apparaitre comme plus complexes que ne le nécessite leur usage premier.
Les exemples contemporains montrent à quel point il paraît difficile d’anticiper les évolutions possibles d’une unité en système métrologique et du point de vue de l’archéologue, déduire des vestiges archéologiques la logique de construction d’un système. En dehors de la raison pratique et arithmétique viennent s’ajouter des volontés économiques, historiques/traditionnelles ou encore diverses de pratiques du quotidien.
Dans une configuration où un système métrologique est exempt de toute logique autre que celle liée à son utilisation pratique et idéelle, on peut estimer qu’il se définit comme l’extrapolation directe d’une unité en fonction d’un système de comptage donné. En partant de ce principe, il est possible de réduire tout système métrologique “simple”293 à une formule arithmétique, tout du moins en ce qui concerne les multiples.
Un système numéral SN sur base N peut alors s’écrire :
SN = {1, 2,…, N, N + 1, N + 2, …, 2N, …}
En partant du principe qu’un système métrologique SM “simple” suit le système numéral, alors, pour une unité U, le système est construit tel quel :
SM = {U, 2.U, …, N.U, (N + 1).U, (N + 2).U, …, 2N.U, …}
Si l’on imagine un système duodécimal, autrement dit base 12 (N = 12), le système numéral donne :
SN = {1, 2, …, N, N + 1, N + 2, …, 2N, …}
autrement dit :
SN = {1, 2, …, 12, (12 + 1), (12 + 2), …, (2×12), …}
En appelant A et B les valeurs 11 et 12 du système duodécimal il est possible de compter ainsi de 1 à 24,
SN = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, A, B, B+1, B+2, …, 2B}
Si les multiples d’une unité métrologique sont construits à partir d’un tel système numéral, les valeurs supérieures à 12 auront tendance à être des multiples de 12. Un multiple 25, s’il est fréquemment utilisé dans un système décimal, n’aurait aucun sens, tout comme 50 et 100.
Si ce procédé de reproduction du système numéral pour créer les multiples d’une unité a tout son sens, notamment pour en faciliter le comptage, il n’en va pas de même pour les fractions. En effet, la façon de se représenter les nombres inférieurs à 1 est particulière, ce qui explique par exemple qu’elle soit généralement abordée bien après les nombres entiers dans l’éducation scolaire.
Les fractions demandent un procédé de visualisation particulier, il est en effet généralement impossible de simplement les “compter” sur le corps. Elle passe dans bien des cas par la représentation d’une forme géométrique, un cercle par exemple, que l’on partage en n parts égales pour visualiser la fraction 1/n (la majorité des graphiques utilisés de nos jours fonctionnent sur ce principe visuel). Ainsi, ce procédé peut aisément s’émanciper du système numéral. Par exemple, si le système décimal représente le socle numéral dans notre société, les fractions les plus communes n’y appartiennent pas (1/4, 1/3, 1/2, 3/4, etc.) alors qu’il est généralement difficile sans outil de visualiser une fraction sur 10 autre que 5/10.
La divisibilité est donc probablement le critère majeur de la création des fractions de la majorité des systèmes métrologiques. Pour cette raison, il est beaucoup plus difficile de détecter la manière dont vont se développer les systèmes de fractions, s’ils sont développés. De nombreux aspects peuvent influer sur la manière de les créer et produire ainsi des résultats très différents. Il semble cependant que les divisions binaires, permettant l’obtention de fractions 1/2, 1/4, 1/8, 1/16 etc., soient les plus faciles à réaliser. La balance à bras égaux favorise grandement la division binaire.
En pratique, l’application stricte d’un système numéral à la création d’un ensemble de fractions d’une unité relève le plus souvent d’une démarche de multiplication que de division. Cela est par exemple le cas de certaines unités pondérales basées sur des graines (comme la graine de caroubier qui a donné le carat ou le takou possiblement utilisé par les Akans) qui sont trop faibles et, contrairement à l’idée répandue, trop hétérogènes pour servir d’unité fonctionnelle294. Plutôt qu’être utilisées au quotidien comme unité usuelle, une unité plus lourde est créée et c’est celle-ci qui va servir de fondation au système métrologique. L’unité minimale (graine de carat, takou ou autre) représente alors une fraction dans le système métrologique, bien qu’elle soit en réalité à l’origine de sa création. Chez les Akans, par exemple, le takou représente entre 1/44 et 1/80 des unités pondérales en usage295. La différence se situe cependant dans l’ordre de construction du système métrologique. Dans un cas, une fraction va être développée à partir d’une unité et va avoir alors tendance à ignorer le système numéral pour suivre une volonté de maniabilité. Dans le second cas, l’unité usuelle est conçue par multiplication d’une unité minimale et non usuelle qui devient alors une fraction du système métrologique. L’usage de la multiplication permet alors de suivre le système numéral.
L’exemple des unités de quantité des Paiwan (Taïwan) peut illustrer cela. L’unité supérieure de leur système métrologique est le talalakan, qui correspond à trois tovliut. L’unité supérieure est donc obtenue par multiplication selon un système numéral, ternaire dans ce cas-là. Or, une unité minimale, bien plus réduite mais non usuelle, existe car chaque tovliut correspond à une poignée de graines de millet296. Le grain de millet correspond alors à l’unité minimale et non usuelle d’un système métrologique créé par multiplication de celle-ci.
La maniabilité du système avant tout,
une théorie viable ?
Les sociétés de l’âge du Bronze de Méditerranée orientale utilisent depuis le IIIe millénaire a.C. des systèmes basés essentiellement sur les divisions de grandes unités plutôt que la multiplication de petites. L’un des arguments souvent avancé pour expliquer ce choix est la maniabilité du nombre 60, comme nous l’avons déjà mentionné, permettant la réalisation de nombreuses fractions. Cependant, si le ratio talent-mine et mine-shekel est dans plusieurs cas de 60 : 1, il ne s’agit toutefois pas d’une situation systématique. La mine de 470 g est notamment divisée en 50 shekels de 9,4 g à Ougarit et sur l’actuelle côte syrienne, et en 40 shekels de 11,75 g par les Hittites.
Mais est-il admissible d’appliquer ce principe de logique arithmétique essentiel, si tant est qu’il soit juste de l’admettre en Méditerranée orientale, pour le monde protohistorique occidental ? Les deux mondes présentent des faciès très différents, en particulier dans le domaine de l’administration politique et économique. Les états à fonctionnement vertical dont l’économie repose notamment sur un système de prélèvement d’impôts, sous forme monétaire ou matérielle, tendent à développer des outils d’administration tels que l’écriture et la métrologie. Ces supports sont en effet essentiels à la réalisation de comptes permettant l’homogénéisation et l’équitabilité des processus. Dans cette optique, le système numéral et l’arithmétique se trouvent nécessairement au centre des procédés. Comme toute technologie, l’amélioration de celle-ci peut entrainer un gain de temps, une facilitation des opérations et/ou un renforcement de la rentabilité.
Les populations de l’Europe occidentale protohistorique, tout du moins jusqu’à la toute fin du Second âge du Fer, ne rentrent pas dans ce schéma fonctionnel. La hiérarchisation existe très clairement dès le Néolithique, les élites en place soumettent peut-être leurs sujets ou leurs clients à des formes d’imposition, mais l’échelle de fonctionnement ne semble pas avoir entraîné le besoin d’une administration poussée avant la fin de la période297. Il est possible que certains outils de compte existent dans ces aires chrono-géographiques. On trouve notamment certains tessons de céramiques retaillés pouvant être réutilisés comme des jetons de compte et les populations de la péninsule Ibérique pratiquent l’écriture durant le second âge du Fer, bien qu’il soit probable qu’elles n’aient jamais eu recours aux signes numéraux et métrologiques298.
L’absence d’une comptabilité écrite montre probablement que ces populations ne sont pas rentrées dans une abstraction des mathématiques amenant à manier des nombres qui ne soient pas directement quantifiables à l’œil. En effet, si dans nos sociétés actuelles nous sommes capables de compter indéfiniment grâce à un système numéral décimal abstrait très catégorisé et efficient, la plupart des nombres restent de l’ordre de l’idée. Ce palier est bien évidemment propre à chacun et si certains sont dépassés au bout de quelques dizaines, certains individus sont capables d’appréhender en quelques secondes des nombres plus élevés.
Il est certainement possible d’admettre que, sans l’appui d’une base matérielle, les fractions sur base 60 sont impossibles à appréhender. Par conséquent, il est hasardeux d’envisager que les populations de l’Europe occidentale manient de telles fractions aux âges des Métaux par simple mimétisme de la Méditerranée orientale. Les procédés mathématiques sont propres au développement de chaque groupe humain et ne peuvent être comparés avec simplicité. Faire l’hypothèse de l’utilisation des systèmes numéraux et de l’arithmétique hautement complexes par une population sur l’argument que d’autres les manient au même moment à 5000 km de distance, même si des contacts existent entre les deux, semble ardu.
Quelles bases de travail privilégier ?
Comment approcher alors les systèmes métrologiques de populations dont on ne connait pas les systèmes numéraux, ni les unités employées ? Sur quelles bases appuyer un travail de métrologie archéologique ?
Les exemples historiographiques des trente dernières années montrent que cette discipline s’est renouvelée notamment en adoptant ou en créant des outils d’analyse de la donnée métrologique archéologique. Cependant, ces développements sont grandement liés à l’étude des populations évoluant dans des États fortement administrés (Minoens, Mycéniens, Mésopotamie, Anatolie, côte syro-palestienienne etc.) où la pratique pondérale s’inscrit probablement dans un ensemble d’outils que l’entité politique contrôle et modère au moins en partie. Dans la majorité des cas, l’étude des populations protohistoriques s’est appuyée sur la comparaison avec ces systèmes, avec toutes les limites que cela implique.
D’un point de vue archéologique, la situation est complexe car en l’absence de sources écrites, les systèmes numéraux, les systèmes métrologiques, les poids de balance et parfois même les produits finis pondérés sont entremêlés et difficiles à dissocier. Certains éléments peuvent aider à y voir plus clair, tels que les marques numérales sur les objets, bien que rares dans notre zone d’étude299, qui permettent de donner un ou plusieurs points de repère à un système métrologique. Le sens métrologique et l’utilité de la mesure et de la normalisation pondérale ne peuvent donc se comprendre qu’en démêlant un à un ces différents éléments. Il est possible de se représenter l’unité métrologique comme la plus petite d’une série d’éléments gigognes et donc le composant le plus fin interprétable (fig. 1-26). Cependant, si la détermination de son existence ou non est un résultat important en soi, cette information n’est pas nécessairement celle qui nous en apprend le plus sur la société étudiée. Mis à part d’éventuels ajustements pour correspondre à celle d’une zone voisine ou d’un partenaire commercial, l’unité métrologique n’est porteuse que d’une information très limitée, presque anodine. Dans un grand nombre de sociétés, elle est créée de manière arbitraire, à l’inverse de la construction théorique ayant produit le système métrique, et n’a donc pas nécessairement une logique intrinsèque autre que celle de son choix.
En revanche, l’étude des autres niveaux d’empilement de l’information métrologique sont porteurs de nombreuses informations, dont les capacités cognitives des populations, les intervalles de grandeurs mesurés, la complexité de la pratique, son usage dans un cadre uniquement privé ou au contraire public… Les systèmes numéraux utilisés, les modalités de construction des systèmes métrologiques et les contextes d’utilisation promettent ainsi beaucoup plus d’apports aux sciences humaines que de tenter de savoir quel modèle a servi à la détermination d’une unité isolée. Par conséquent, l’étude des instruments de pesée ne doit pas, ou ne devrait pas, avoir pour objectif la recherche de l’unité pondérale comme finalité.
II. Masse et pesée, processus abstraits
et connaissances empiriques
Nous l’avons tout juste effleuré mais, au sein des systèmes métrologiques, la mesure de la masse possède des particularités qui la rendent tout à fait singulière. Ces caractéristiques font qu’il est nécessaire de prendre un certain recul lorsqu’on étudie les instruments de pesée pour éviter de tomber dans la déclaration moderno-centrées. La gymnastique mentale obligatoire pour cela est une preuve de plus de l’ancrage particulier que les systèmes numéraux et métrologiques tiennent dans les sociétés.
1. Des concepts universels ?
Bien qu’elle soit rarement décrite de cette manière, la pesée est une technologie reposant sur un certain nombre de concepts abstraits et plusieurs outils distincts. De ce fait, elle ne peut pas être abordée comme un procédé universel que toute société a été amenée à manipuler. L’association déterministe entre pesée, commerce et monnaie, en particulier, est loin d’être valable universellement et amène aisément à des raisonnements circulaires lorsqu’il s’agit d’étudier les sociétés protohistoriques.
Masse et poids, entre conceptualisation et empirisme
La masse et le poids font l’objet aujourd’hui d’une confusion à grande échelle à laquelle il est difficile d’échapper. Pour cela, il semble nécessaire de revenir dans un premier temps sur la définition de ces deux termes.
La masse est une valeur immuable, dépendante de la quantité de matière et de la densité d’un sujet, dont l’unité de référence dans le système international est le kilogramme. Le poids, quant à lui, est une force, mesurée en newtons, égale au produit de la masse et de l’accélération de la pesanteur (9,81 m/s2 en moyenne sur Terre). Celui-ci est donc dépendant de la gravité qui varie sensiblement sur la Terre, notamment en fonction de l’altitude. Ainsi, un individu ayant une masse de 70 kg possèdera sur Terre un poids d’environ 686,5 N.
La masse et le poids sont difficilement dissociables et dans le langage courant nous tendons à confondre les deux termes. Cette distinction, mise en évidence au milieu du XVIIIe s. par I. Newton300, peine à rentrer dans le vocabulaire courant, mais cette confusion ne devrait pas être répercutée dans la littérature scientifique, qu’il s’agisse de sciences humaines ou non, et encore moins lorsque le sujet d’étude est la métrologie pondérale.
Il faut cependant ajouter à cela que la masse est aujourd’hui calculée par le biais du poids exercé par l’objet pesé sur le plateau de la balance, qu’elle soit mécanique ou électronique. Ainsi, si nous ne pouvons pas parler d’un poids exprimé en grammes ou kilogrammes sans tomber dans l’erreur scientifique, il est certain que ces deux grandeurs, masse et poids, devaient être perçues comme un seul phénomène durant la Protohistoire.
Dans le champ des mesures, la masse occupe une place particulière. Les concepts de longueur et de capacité partagent le trait commun d’être observables avant d’être mesurables, au travers d’un seul et même sens : la vue. La masse, quant à elle, échappe à ce domaine de la vision et ne peut être appréhendée qu’au travers d’un processus plus délicat faisant appel au sens du toucher. C’est le cas lorsque nous soupesons un objet. Par conséquent, si nous considérons aujourd’hui la masse comme la caractéristique invariable et mesurable d’un corps, rien ne permet d’affirmer que ces concepts soient partagés universellement. En l’absence d’instruments dédiés à son observation, elle peut échapper totalement au spectre des caractéristiques commensurables.
La pesée, une pratique multifonctionnelle
En dehors de cet aspect cognitif et théorique, il est clair que la pesée n’est pas non plus une pratique partagée par toutes les sociétés, indépendamment de leur niveau de hiérarchisation sociale ou de la complexité de leurs échanges économiques. C’est par exemple le cas aujourd’hui du peuple des Aoheng (Bornéo, Indonésie), une communauté de moins de 3 000 individus, dont l’économie repose sur la culture du riz. Malgré une ouverture avec l’extérieur et l’existence d’échanges commerciaux, les membres de ce groupe ne développent aucune pratique pondérale. Lorsque le poids ou la masse sont envisagés, c’est selon un rapport entre une mesure de capacité et une densité approximative (le riz décortiqué est par exemple considéré comme 60 % plus dense que le riz non décortiqué) ou encore selon un concept de charge transportable301. L’ethnologie comme l’histoire le montrent bien, et même lorsque des groupes humains pratiquent la pesée, celle-ci peut être effectuée dans des cadres très spécifiques qui diffèrent des contextes rigides proposés dans la littérature scientifique pour les populations protohistoriques. Chez les Akan, un ensemble de peuple du sud du Ghana et du sud-est de la Côte d’Ivoire, par exemple, la pesée acquiert au XVIIIe s. une fonction toute spécifique : indiquer le prix d’un paiement exprimé en poudre d’or. Ainsi, si les produits échangés ne font pas l’objet d’une pesée, mais sont délivrés selon des quantités traditionnelles, la poudre d’or en revanche est pesée par le vendeur et l’acheteur. Le prix du produit est donc spécifié au travers de la masse d’or et la monnaie est représentée par la poudre d’or elle-même302.
En Occident aujourd’hui, lorsque l’on pense à la pesée ou à son instrument, la balance, plusieurs images viennent en tête. L’une d’entre elle est effectivement liée au commerce ; il s’agit de la balance sur les marchés ou pour peser les fruits et légumes dans les supermarchés. Mais il faut bien reconnaître que notre rapport à la pesée commerciale s’arrête bien souvent à ces deux cas pour la majorité d’entre nous. La balance est cependant présente dans d’autres sphères, associée à d’autres idées : la balance de la justice, la balance de cuisine ou encore le pèse-personne. Il est donc évident qu’à partir du moment où l’idée est acceptée que la pesée peut concerner tout objet physique, il serait bien réducteur de la croire restreinte à la seule pesée commerciale.
La mesure pondérale implique l’usage d’une balance, elle n’oblige cependant en rien à l’utilisation de poids et de systèmes métrologiques. Le Roux montre par exemple, à propos des Jawi (Thaïlande), un peuple d’agriculteurs, qu’ils appréhendent mal le concept de masse. Ainsi, celle-ci s’exprime à travers une capacité et mélange le matériau mesuré, le contenant dont la capacité est connue et l’équilibre de la balance303.
Il existe ainsi un grand nombre de situations distinctes qui amènent à faire appel à la pratique pondérale. Celle-ci peut servir à comparer des quantités ou des densités, mesurer la masse d’un produit échangé ou d’un moyen de paiement. Elle peut dans certains cas être effectuée pour n’importe quelle transaction ou mesure ou au contraire être réservée à un type d’opération spécifique. Il est donc a priori impossible d’attribuer à la balance une fonction sociale ou économique particulière pour l’Europe protohistorique alors que les exemples ethnographiques montrent le large spectre de ses utilisations.
2. La balance, l’illusion de la précision ?
Lorsqu’il s’agit d’aborder le thème de la précision des balances, il n’est pas rare de trouver nombre d’informations contradictoires dans la littérature scientifique, souvent peu argumentées. Cela peut aller de l’identification d’une unité au milligramme304 ou au contraire de l’acceptation de 20 % de tolérance dans la conception de poids de balance. Les travaux qui s’appuient sur une véritable analyse des caractéristiques techniques des balances, et par conséquent de leurs possibles failles, restent en comparaison bien rares. Pour cette raison, il semble utile de revenir sur quelques principes mécaniques afin de mieux comprendre et appréhender les facteurs pouvant influer sur la précision des balances anciennes.
La loi de levier
En 1680 est inventée par un certain Monsieur Bardonneau, “Maître Balancier à Limoges”305, la première balance automatique, autrement dit, une balance dépourvue de poids sur laquelle il est possible de lire directement la masse du corps pesé. Avant cela, le principe de toutes les balances repose sur ce qui est en partie théorisé par Archimède (De l’équilibre des figures planes) comme la loi du levier. Le levier en question est un segment rigide se déplaçant autour d’un pivot. L’équilibre, autrement dit la mise à l’horizontale du levier, se produit lorsque les moments des forces exercées sur chaque bras du levier sont égaux.
En prenant l’exemple d’un levier divisé par son point de pivot en deux segments de longueurs A et B aux extrémités desquels sont respectivement exercées des forces P1 et P2, on obtient deux moments de ces forces, A.P1 (A × P1) et B.P2 (B × P2). Le levier s’équilibre lorsque A.P1 = B.P2 (fig. 1-27).
Dans le vocabulaire courant, le terme de levier est surtout désigné pour sa capacité à permettre de soulever un objet dont le poids306 est supérieur à la force utilisée pour le mouvoir. Pour prendre un exemple de simple rappel, imaginons un levier mesurant 4 m, avec un point de pivot le divisant selon un ratio 3/4 : 1/4, autrement dit A = 3 m et B = 1 m. Si un objet exerce à l’extrémité de B une force P2 de 2100 N (soit 214,14 kg), alors pour faire déplacer l’objet en question, il est nécessaire que A.P1 soit supérieur à B.P2, soit,
P1 > B.P2 ÷ A
P1 > 1 × 2100 ÷ 3
P1 > 700
En exerçant une force supérieure 700 N à l’extrémité du côté long du levier, il est ainsi possible de déplacer l’objet disposé en son extrémité courte. En d’autres termes, un individu ayant une masse supérieure à 72 kg pourra en déplacer plus de 200 en utilisant un bras de levier dont le point de pivot est disposé selon le ratio 3/4 : 1/4.
La balance à deux bras égaux repose sur le même principe mais en utilisant un point de pivot disposé exactement au centre du levier. Elle permet donc de vérifier l’égalité des poids exercés sur chaque plateau lorsque le levier, ou fléau, trouve l’équilibre et par conséquent, l’égalité de leurs masses.
La balance dite “romaine” à contrepoids mobile fonctionne quant à elle sur le principe de proportionnalité entre les longueurs des bras du fléau et les forces exercées pour obtenir l’équilibre. Elle semble être originaire du domaine Italique307, tout du moins dans sa forme connue aujourd’hui, et dont les exemplaires les plus anciens ne semblent pas antérieurs au IIe s. a.C.308.
Pour reprendre l’exemple proposé plus haut, si A = 3 × B alors, l’équilibre se fait lorsque P2 = 3 × P1. Elle nécessite ainsi de connaître précisément deux constantes (A et P1) et de faire changer une variable (B) pour obtenir l’équilibre (fig. 1-28). Cette méthode a l’avantage de la rapidité, il est possible de lire une mesure en faisant simplement glisser un peson, alors qu’une balance à deux bras impose d’enlever et rajouter des poids de valeurs différentes jusqu’à obtention de la bonne mesure. En revanche, elle peut entrainer certains problèmes de précision et de vérification.
Les quatre qualités d’une balance :
force, sensibilité, justesse et fidélité
En mécanique, il est communément associées quatre qualités principales aux balances à bras bien qu’elles ne soient pas clairement spécifiées telles quelles dans la littérature scientifique. De ces quatre caractéristiques dépendent les mesures qui seront effectuées par l’appareil.
La première qualité d’une balance est sa force, autrement dit, le poids maximum qu’elle peut supporter sans se détériorer. Dans nos actuelles balances électroniques, celle-ci est mentionnée et entraîne généralement un message d’erreur lorsqu’elles sont dépassées. En ce qui concerne une balance à bras, cela dépend essentiellement de la taille, de la résistance et de l’élasticité du matériau employé pour créer le fléau. En effet, toute déformation de celui-ci peut entraîner un déplacement de son centre de gravité et ainsi modifier sa fiabilité.
Deuxièmement, c’est la sensibilité qui détermine le fonctionnement d’une balance. Celle-ci est étroitement lié à ce que l’on définit comme sa précision. La sensibilité est la capacité d’une balance, indépendamment de son type, à “trébucher”309, à réagir, à partir d’une certaine force exercée sur le plateau ou l’un des plateaux. Plus la force ou le poids nécessaire sera faible, plus la balance sera sensible. E. Sperber a par exemple démontré que pour trois balances à bras égaux vikings à vide (fig. 1-29), la sensibilité correspondait à 0,2-0,4 g pour une déflexion du haut de l’aiguille de 1mm par rapport à la position zéro (verticale)310. On notera ici qu’aucun exemplaire de fléau de balance protohistorique identifié ne possède d’aiguille mais que certains pouvaient tout à fait posséder un fil à plomb remplissant la même fonction de contrôle de l’horizontalité du fléau par observation de la perpendiculaire à la verticale (fig. 1-30). L’autre différence d’importance entre ces fléaux et ceux de l’époque viking est l’éloignement du point de support par rapport au fléau dans le cas de ces dernières.

La troisième caractéristique, qui est probablement la plus fréquemment abordée en métrologie historique ou archéologique, est la notion de justesse. Elle est également une composante de la précision et correspond à la faculté d’une balance à bras égaux ou une balance romaine à présenter un équilibre lorsque les poids exercés de part et d’autre du fléau sont strictement égaux311. Dans le cas d’une balance à bras égaux, la justesse va dépendre de plusieurs critères, la stricte égalité des bras en longueur, en densité et en masse, le bon positionnement du joug et des fixations, l’égalité des masses des plateaux et des fixations. Dans le cas d’une balance romaine, c’est de l’exactitude des mesures de longueur sur le bras accueillant le contrepoids mobile que dépendra la justesse. La meilleure méthode de confirmation de la justesse est la capacité à trouver l’équilibre en disposant deux masses égales sur chaque plateau et de retrouver cet équilibre en transposant ensuite les poids d’un plateau à l’autre312. Il est intéressant de noter que ce test ne peut en aucun cas être effectué sur une balance romaine ou tout d’autre type de balance asymétrique.
La dernière qualité majeure d’une balance, indépendamment de sa nature est sa capacité à obtenir le même résultat en reproduisant plusieurs fois la même mesure. On parle alors de fidélité de l’appareil. Plusieurs aspects peuvent être à l’origine d’une mauvaise fidélité : la déformation des matériaux, les contraintes mécaniques de la balance, etc.
Par conséquent, afin de s’interroger sur la précision des instruments de pesée et leurs potentiels facteurs d’erreurs, il est nécessaire de tenir compte de ces différentes qualités et de ce qui influe sur elles. En gardant en tête les propriétés mécaniques des balances, il est également possible de mieux appréhender les concepts abordés plus haut et le caractère universel ou non des concepts de masse et de pesée.
Propriétés mécaniques des balances
et facteurs d’erreurs
Il est question ici de revenir brièvement sur les propriétés mécaniques des balances à deux bras égaux, leur fonctionnement d’un point de vue pratique et les facteurs pouvant les rendre involontairement ou volontairement fausses. Cet aspect est primordial car aucun discours cohérent ne peut être tenu sur la métrologie sans s’interroger au préalable sur les balances utilisées pour peser et fabriquer des poids considérés justes.
En termes de métrologie archéologique, E. Sperber est probablement celui qui est allé le plus loin dans l’interrogation des propriétés mécaniques des balances retrouvées en contexte archéologique313. Là où ses prédécesseurs avaient procédé à des expérimentations empiriques pour mesurer la sensibilité des balances, E. Sperber propose de la calculer à partir des dimensions des instruments eux-mêmes314. Cette méthode a l’immense avantage d’être applicable à n’importe quel corpus de balance sur la base des seuls dessins et d’estimations de volume et de densité. Il est ainsi possible de résumer en une équation le rapport entre les dimensions d’un fléau de balance et l’angle de déflexion entraîné par la surcharge d’un fléau315, soit :
p représente la différence de masse (en grammes) entre le contenu du plateau 1 et le contenu du plateau 2 ; α est l’angle de déflexion qu’entraîne l’ajout de p ; d1 est la longueur (en mm) entre le point de support du fléau et son centre de gravité ; d2 est la longueur entre ce même point de support et la ligne imaginaire reliant les deux attaches des chaines de suspension des plateaux au fléau ; g est la masse (en grammes) du fléau, L sa longueur et P la masse des éléments de suspension (chaines ou cordes, plateaux etc. ; fig. 1-31).

En possession des dimensions des fléaux de balance, il est alors possible de faire des expérimentions de sensibilité desdites balances en fonction de différentes charges et ainsi approcher la sensibilité de ces instruments. Bien évidemment, ces estimations ne pourront servir qu’à titre d’indications étant donné qu’elles permettront uniquement de proposer des situations types. Il sera donc impossible de déterminer quelles situations sont considérées à la Protohistoire comme une balance équilibrée ou au contraire déséquilibrée, mais ces expériences permettront la mise en place d’un cadre de travail et de comparaison moins opaque et plus propice à l’argumentation.
3. De la balance au lot de poids
Plus haut ont été exposées les méthodes permettant le passage d’une unité à un système métrologique dans toute sa complexité. Sans revenir sur cela, il est possible d’aborder les spécificités des systèmes métrologiques pondéraux en fonction des propriétés mécaniques des balances et surtout leurs implications sur notre interprétation de la donnée archéologique.
L’œuf et la poule – le poids et la balance
Il n’est pas aisé de déterminer qui du concept du poids ou de la balance apparaît en premier ou si les deux sont le résultat d’un seul et même processus qui amène à la création des instruments de pesée dans leur ensemble. Les réponses sont peut-être toutes vraies en fonction des lieux et des époques cependant, certains indices tendent à penser que la balance a, comme c’est probablement le cas chez les Égyptiens, précédé les poids316 alors que parfois la notion de masse existe avant la connaissance de la balance, comme chez les Palawan (Philippines), un peuple d’agriculteur sur brûlis, dont l’économie repose également sur la chasse et la cueillette317.
La balance vient probablement dans un premier temps épauler une pratique de comparaison des masses qui pouvait déjà être réalisée grossièrement à l’aide des bras, des mains ou d’autres éléments “opportunistes”. Il est probable que ce principe ait ensuite été étendu et répliqué grâce aux connaissances empiriques de la loi du levier (voir le chapitre “La loi de levier”, p. 57) qui devait déjà être maîtrisée au quotidien. L’usage de dispositifs tels que les chariots à deux roues permet en effet déjà d’éprouver l’avantage du levier. En Égypte, le chadouf est utilisé probablement depuis le IIIe millénaire a.C.318 comme outil d’irrigation et fonctionne entièrement sur ce principe physique. Ainsi, il est hautement probable que, dans un premier temps, la balance soit un outil permettant la comparaison de deux produits selon leur masse. Il est important de rappeler que la balance ne donne que trois types de résultats, A est plus lourd que B ; A est plus léger que B ; A et B ont la même masse. Le rôle des poids de balance est de venir standardiser les valeurs de A ou B par l’utilisation récurrente d’un objet à la masse fixe qui vient servir de référence. De ce fait, la création d’un étalon et d’un système métrologique normalisés n’est nécessaire que si la pesée fait intervenir deux utilisateurs. Si la pesée est faite dans un cadre privé ou déséquilibré (autrement dit une situation où seul l’un des acteurs doit connaître la valeur des poids, soit en raison d’un statut différent, soit qu’il possède un savoir différent), la création de poids de balance n’a pas pour obligation de suivre une quelconque norme.
Dans l’Iliade, Zeus sort sa balance d’or et pèse les destins d’Achille et d’Hector au travers des Kères (génies ou déesses de la destinée et de la mort) des Akhaiens et Troyens, avec pour conséquence l’annonce de la mort du Troyen (Iliade, chant XXII). La pesée effectuée ici ne fait appel à aucun poids, il s’agit alors d’une simple comparaison, faite dans ce qu’on peut appeler un cadre privé, ici celui des Dieux et de l’Olympe. En revanche, dans la scène bien connue de la pesée de l’âme, dans l’ancienne religion égyptienne, le cœur du défunt est pesé afin de définir s’il est plus lourd ou plus léger qu’une plume (Livre des Morts, chapitre CXXV). Mais on remarquera que si la plume fait office de poids, d’élément de référence, sa masse exacte n’est jamais questionnée, car celle-ci n’est tout simplement pas questionnable. La pesée est effectuée dans un cadre que l’on peut définir comme déséquilibré puisque seul le peseur connaît la valeur de l’étalon.
Si ces exemples sont tous deux issus de la mythologie et s’inscrivent dans une aire géographique différente de celle étudiée ici, ce n’est pas pour autant qu’elles ne peuvent pas y être transposées. En effet, elles font état d’un fonctionnement très basique de la balance, très simplifié, où l’outil ne s’embarrasse pas de l’usage de connaissances arithmétiques ou d’une normalisation quelconque de l’outil pondéral. La balance est en effet prise pour ce qu’elle est, un outil de comparaison.
Le poids de balance, pour sa part, englobe l’idée d’un référent plus ou moins précis applicable dans un certain domaine. Celui-ci peut prendre forme sans qu’une mesure explicite vienne le caractériser précisément. Un exemple est le tibung (“unité de charge”) maniée par les Palawan (voir plus haut), qui correspond à la charge maximale qu’un homme peut porter sur une distance longue319. Cette charge, cette masse, existe, elle est connue, appréhendée, appliquée et parfois nommée, mais n’est pas nécessairement pesée, mesurée en tant que telle.
Il ne faut cependant qu’un pas pour que cette pratique soit simplifiée en utilisant un référent stable, puis un pas de plus pour que celui-ci soit dupliqué avec plus ou moins de complexité en un système métrologique. La pratique pondérale, telle qu’on l’entend en général, unit de manière assez indissociable poids et balance, cependant, ces deux outils font appels à des processus d’abstraction différents et peuvent tout à fait être utilisés séparément.
Le système pondéral : une idée et une forme
La particularité notable d’un système métrologique pondéral est la manière dont il prend matériellement forme. Tout le monde a en tête l’image des balances Roberval avec leur jeu de poids de balance en laiton, du plus petit au plus gros. Généralement, aucun des poids du lot n’apparaît en double et chaque multiple et fraction n’y sont pas représentés. La raison à cela est très simple, un ensemble de peseur peut rapidement devenir très lourd et donc intransportable. D’un point de vue uniquement arithmétique, la constitution d’un lot de poids de balance va donc être conditionnée par quatre impératifs : l’unité ou les unités, le système numéral, l’intuitivité des fractions et la rationalisation du lot pour qu’il contienne un minimum de poids.
L’ensemble des sources historiques, ethnologiques et archéologiques mentionnées jusqu’ici, ne montre aucun cas de matérialisation stricte de toutes les fractions et tous les multiples d’un système métrologique donné, mais dégage plutôt l’image d’une volonté de maniabilité et de rationalisation des lots de peseur afin qu’ils permettent de réaliser un maximum d’opérations de mesure avec un minimum de poids de balance. Pour prendre un exemple, si l’unité et le triple de celle-ci sont matérialisés sous la forme de poids, le quadruple peut, quant à lui, être obtenu par l’addition des deux et ne nécessite donc pas d’être fabriqué. Cette logique dépend grandement du type de balance utilisé et de la manière dont elle est utilisée. En effet, sur une balance à deux bras égaux et deux plateaux, si l’addition est possible (fig. 1-32-b), la soustraction l’est aussi en posant le poids à soustraire sur le même plateau que le produit pesé (fig. 1-32-c). Les balances “romaines”, à contrepoids, utilisent un principe différent, décrit plus haut (voir le chapitre “La loi de levier”, p. 57), et vont faire appel à des logiques différentes. Le contrepoids et la balance sont généralement indissociables ou nécessitent l’utilisation d’un poids de référence permettant de confirmer la validité du système de mesure. La matérialisation du système métrologique va alors prendre forme sur la balance elle-même et il peut être relativement indépendant des problèmes de masse totale du lot de peseur. Enfin, des balances que l’on pourrait définir comme hybrides ont probablement également existé, cela est peut-être le cas du fléau en bronze trouvé dans l’habitat du Ve s. a.C. de Hochdorf (Baden-Württemberg, Allemagne). Bien qu’il s’agisse clairement d’un fléau de balance à deux bras égaux, celui-ci a la particularité de présenter une série de graduations sur l’un de ses bras
(fig. 1-33). Un tel dispositif pourrait permettre de combiner les caractéristiques d’une balance à deux bras égaux et d’une balance “romaine”.
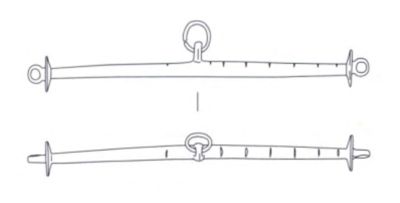
Par conséquent, les instruments de pesée ne peuvent être compris qu’en tenant compte de la complexité des processus qui participent à leur conception et à leur utilisation. Analyser un poids de balance ou un fléau retrouvé de manière isolée, c’est accepter l’idée qu’il s’agit d’une donnée incomplète. La métrologie archéologique se doit donc de composer avec le manque d’information et ne permet pas toujours de reconstituer la totalité des strates qui constituent les instruments de pesée et les systèmes métrologiques pondéraux.
À chaque problème sa solution
I. Classer la donnée
Le classement typologique des instruments de pesée des âges des Métaux n’est pas une mince affaire. Les poids de balance, en particulier, présentent un caractère polymorphe très prononcé et une grande variabilité morphologique qui découle de l’étendue géographique du corpus, de la large plage chronologique prise en considération mais également de la faible standardisation typologique qui peut exister au sein de mêmes ensembles voire de mêmes lots.
Pour ces raisons, un classement purement morphologique est difficile et amène plus à scinder le corpus qu’à regrouper des éléments similaires. Un classement par matériau n’aurait que peu de sens étant donné que certains objets, parfois au sein de mêmes lots, sont de types similaires mais faits dans des matériaux distincts. Le classement le plus efficient serait a priori celui des modes d’utilisation des poids (par suspension, par “enfilage” ou par pose). Cependant, une telle distinction s’avère avant tout interprétative, notamment à propos du type de balance employé, et certains objets sont difficiles à classer de manière exclusive dans l’une ou l’autre de ces catégories. En effet, les objets perforés peuvent en réalité être enfilés ou suspendus, la plupart peuvent également être posés, tout comme une grande partie des objets à bélière que nous pourrions penser destinés à être suspendus. Ce travail minutieux de typologie est essentiel et nécessitera d’être effectué. Toutefois, dans le cadre de cet ouvrage, une telle tâche n’a pu être menée malgré toute l’aide que j’ai pu recevoir.
Afin de tout de même classer ces artefacts de manière minimale, nous définirons ici cinq groupes principaux mélangeant critères fonctionnels et morphologiques. Ils correspondent aux cinq catégories identifiées par l’historiographie des XIXe et XXe s. : les poids piriformes, les poids lenticulaires, les poids quadrangulaires, les poids cylindroïdes et les poids sphériques (fig. 1-34). À ces grands types, nous ajouterons une catégorie de poids opportunistes dont l’utilisation consiste à la réutilisation d’objets avec peu ou sans mise en forme. Enfin, certains objets dont l’identification comme poids est envisagée ne rentrent dans aucune de ces grandes catégories mais ils ne sont pas suffisamment nombreux pour permettre de définir d’autres types.
Au sein de chacun de ces types, nous distinguons plusieurs variantes. Ainsi, nous trouvons au sein des poids piriformes des poids à bélière de formes diverses, avec ou sans surface de pose plane, munis d’une bélière aménagée dans l’objet avec ou sans ajout de matériaux ou fait d’une tige ou d’une boucle insérée dans l’objet (fig. 1-35). Le terme piriforme est ici pris dans un sens très large à défaut d’en trouver un plus adapté, en reprenant la terminologie (pear-shaped) proposée par C. Pare pour ces objets320. Nous y incluons des artefacts dont la base peut-être aussi bien circulaire que quadrangulaire et dont le profil piriforme peut-être net ou simplement marqué par l’existence d’un bouton ou d’une bélière sommitale. Il s’agit généralement des poids qui renvoient le plus aisément à leur catégorie fonctionnelle dans l’esprit collectif en raison de leur similarité avec les poids romains ou ceux en laiton encore utilisés jusqu’à récemment avec des balances à bras.
Les poids lenticulaires varient d’une forme oblongue à une forme à proprement parler lenticulaire et peuvent être munis d’une gorge sur le pourtour de l’objet et/ou de cupules plus ou moins larges et étroites sur leurs faces (fig. 1-36).
Les poids quadrangulaires peuvent être des parallélépipèdes, des cubes ou des polyèdres. Certains d’entre eux présentent un décor incisé ou incrusté de lignes sinusoïdales (fig. 1-37).
Parmi les poids cylindroïdes, certains disposent d’une perforation centrale alors que d’autres en sont dépourvus. Leur forme générale peut être celle d’un disque fin ou épais, d’un tronc de cône, d’un double tronc de cône ou encore d’un cylindre. Certains d’entre eux présentent des côtés concaves ou annelés (fig. 1-38).
Enfin, les poids sphériques peuvent correspondre à des sphères parfaites, avec ou sans méplat, ou posséder une forme ovoïde ou de sphère imparfaite. Certains présentent des excroissances. Dans d’autres cas, la sphère est double ou triple (fig. 1-39).
Les plateaux apparaissent dans des quantités beaucoup moins élevées dans le registre archéologique de l’Europe protohistorique. Nous en identifions globalement deux types, chacun composé de variantes en fonction du nombre de perforations de suspension. Les plateaux plats ou à concavité faible et les plateaux creux (fig. 1-40). La distinction entre ces types n’est pas à proprement parler binaire et il est parfois difficile de déterminer clairement à partir de quelle concavité nous pouvons réellement parler de plateaux creux. Dans la majorité des cas, ces plateaux disposent de 3 ou 4 perforations de suspensions mais nous constatons des situations ou ces perforations sont plus nombreuses voire où ces plateaux sont uniquement pourvus d’une perforation centrale. Nous reviendrons sur les implications technologiques de ces choix.
Les fléaux offrent une variété à peine plus grande. Leur distinction se fait uniquement sur des critères morphologiques. La plupart des fléaux présentent une section circulaire et un léger renflement dans leur partie centrale. Nous trouvons toutefois trois types d’extrémités différentes : des extrémités simples terminées par un rétrécissement du diamètre du fléau (fig. 1-41-a), des extrémités à renflements caractérisées au contraire par une augmentation sensible du diamètre qui peut alors prendre une forme carénée ou globulaire (fig. 1-41-b) et enfin des extrémités discoïdes marquées par une forte augmentation du diamètre en forme d’embouchure de trompette (fig. 1-41-c). Un quatrième et dernier type, connu jusqu’à ce jour par un seul exemplaire clairement identifié, correspond à un fléau de forme et de profil rectangulaire (fig. 1-41-d). Un élément caractéristique de certains fléaux de l’âge du Bronze est une sorte de goupille en alliage cuivreux, ayant la forme d’un oméga étiré en hauteur (fig. 1-42). Ce dispositif, bien que disparu dans certains cas, semble associé à tous les types identifiés pour cette période.

Nous trouvons également des variantes dans ces types en fonction de la forme et de l’orientation des perforation distales des fléaux permettant l’assujettissement des dispositifs de suspension. Ces perforations peuvent être verticales ou obliques. Dans au moins un cas, nous pouvons suspecter que la perforation centrale du fléau, généralement verticale, est disposée de manière horizontale.
II. Étudier une pratique métrologique
à partir d’artefacts archéologiques
La pratique métrologique se construit sur un fonds conceptuel ancré profondément dans les sphères du culturel et du social. Dans le cas qui nous intéresse ici, cette abstraction intellectuelle prend corps dans le domaine du matériel sous la forme d’une panoplie d’outils. Si la balance est la clé de voûte de la pesée, son expression même, ce sont les poids qui vont venir interpréter et représenter le cadre métrologique choisi par un groupe humain ou un monde social donné. Si l’étude conjointe de ces deux types d’instruments est évidemment la plus à même d’apporter un maximum de finesse dans les résultats, leur association archéologique est rare et leur nature n’est pas sans poser un certain nombre de problèmes.
1. Masse idéelle, masse réelle et masse actuelle
En premier lieu, il est nécessaire de s’interroger sur ce qu’est un poids de balance en tant qu’artefact. Si nous avons pu décrire rapidement les processus cognitifs qui permettent de construire les concepts de la mesure pondérale et l’idée du poids de balance, la création de l’artefact lui-même amène d’autres questions matérielles et techniques.
De l’idée à l’objet
Une fois que l’unité pondérale et le système numéral/métrologique sont choisis, l’enjeu est encore de donner forme aux instruments de pesée et en particulier aux poids de balance. Plusieurs cas de figure sont alors possibles : la création d’un objet “ex-nihilo”, la reproduction à partir d’un étalon de référence ou la copie de n’importe quel objet dont la masse correspond à l’unité. Chaque cas de figure va avoir des répercussions différentes sur le rapport entre la “masse idéelle”, la masse théorique que doit représenter le poids de balance, et la “masse de conception”, celle que ce dernier aura à la fin de la chaîne opératoire. Nous pouvons considérer que, à moins d’une intention réelle de contrefaçon, l’opérateur va toujours chercher à obtenir une équivalence parfaite entre la masse voulue et la masse obtenue dans la limite de ses compétences techniques et des prérequis sociaux et économiques321.
Le cas le plus simple, et peut-être le plus répandu pour les périodes historiques, est celui de la copie d’un étalon de référence. C’est en effet le cas dans la majorité des sociétés où la fiabilité métrologique est garantie par une institution comme à Rome où les étalons de masse sont conservés dans le temple de Castor322, à Athènes dans le trésor d’Athéna323 ou encore le prototype international du kilogramme, conservé jusqu’à récemment sous une triple cloche de verre au Bureau International des Poids et Mesures (Parc de Saint-Cloud, Hauts-de-Seine, France). Il est à noter que ce dernier, qui prend la forme d’un cylindre fait de platine et d’iridium a laissé sa place, il y a peu de temps, à une nouvelle définition du kilogramme, fondée sur la constante fondamentale de Planck.
L’existence d’un étalon de référence a un impact direct sur la chaîne opératoire de fabrication d’un poids de balance et sur sa réalité matérielle. Dans le cas de la fabrication d’un poids juste (les cas de fraude mis à part), le processus va consister à rassembler dans un premier temps la masse de matière nécessaire à la confection du poids et à contrôler celle-ci au moyen d’une balance. Il est évident que la chaîne opératoire de production d’un poids de balance s’achève par une pesée de contrôle qui doit être validée pour que celui-ci soit utilisable.
Le procédé est rigoureusement le même dans le cas d’une copie d’un objet servant d’étalon “provisoire” mais les conséquences seront sensiblement différentes. Par provisoire, il est question ici d’un objet n’étant pas un étalon officiel auquel sont comparés tous les poids fabriqués, mais un poids de balance destiné à être utilisé et dont la fonction d’étalon de reproduction est opportuniste (fig. 1-43).
Dans les deux cas, l’équation entre “masse idéelle” et “masse réelle” est donc la suivante :
masse réelle = masse idéelle +/- erreur instrumentale
L’erreur instrumentale, celle de la balance, peut amener à des variations plus ou moins grandes comme nous l’avons vu plus haut. Cependant, au moment de sa mise en circulation, un poids de balance est nécessairement estimé juste, à l’exception du cas d’une fraude volontaire. Pour ces raisons, la masse obtenue lors de la création d’un poids de balance n’est jamais exactement la “masse idéelle” telle que la définit C. Pulak dans son travail sur Uluburun et Cap Gelidonya324.
Ce qui constitue la plus grande différence entre ces deux modes de reproduction va se jouer dans la répétition de l’opération à plusieurs reprises (fig. 1-43). Dans le cas de communautés utilisant un étalon de référence auquel sont comparés tous les poids fabriqués, l’erreur instrumentale sera toujours sensiblement la même et la masse obtenue pour les poids de balance sera comprise dans une fourchette relativement faible autour de la masse idéelle. De plus, en cas de litige ou de doute sur la fiabilité d’un poids de balance, il est logiquement possible d’en vérifier la fiabilité en le comparant à l’étalon.
En revanche, lorsque chaque poids est produit par comparaison avec un autre poids de balance d’une valeur équivalente, l’erreur devient cumulative. L’erreur instrumentale est répétée autant de fois qu’un nouvel objet est produit. Celle-ci pouvant être négative ou positive et dépendante de la balance utilisée, il est impossible de prévoir si une réitération du procédé va nous rapprocher ou nous éloigner de la “masse idéelle”. L’équation devient alors :
masse réelle = masse idéelle + (somme des erreurs instrumentales positives et négatives)
Le dernier cas abordé est celui de la création ex-nihilo d’un poids de balance. Force est de reconnaître que nous ne pouvons guère aller bien loin dans la description de ce procédé ou en tout cas dans l’analyse de son influence sur le registre matériel. Tout système métrologique pondéral est nécessairement créé ex nihilo ou copié. Dans la majorité des cas renseignés, la création d’un système métrologique s’inspire ou imite des éléments reconnaissables du quotidien : graines de takou chez les Akan325, broches (obeloi) chez les grecs326, etc.
L’une des principales difficultés de l’étude des métrologies anciennes est justement de distinguer un système métrologique créé ex-nihilo d’un système copié, dévié ou adapté. En termes d’implication sur le registre matériel, il faut noter que deux situations sont envisageables : la première est que le système est basé sur une unité jugée fiable et pérenne, comme les graines des Akans, et qu’à chaque fabrication d’un poids de balance, une nouvelle mesure de cette unité est faite, impliquant le cumul d’une erreur liée à la variabilité de la masse d’un objet issu de la nature ; la deuxième consiste à revenir à l’un des deux premiers points exposés, autrement dit la création d’un étalon de référence ou la copie de poids à poids.
Du poids aux poids :
la création de fractions et de multiples
Cette cumulation des erreurs instrumentales n’est pas propre qu’aux unités d’un système métrologique mais à toutes ses composantes, fractions et multiples inclus. De la même façon qu’il existe différentes manières de créer un poids de balance égal à une unité, plusieurs choix s’offrent à celui désirant fabriquer des fractions et des multiples de celui-ci. L’objectif ici n’est pas tant d’aborder les spécificités technologiques de la création des poids de balance durant la Protohistoire mais de comprendre comment certains faits et limites techniques influenceront différemment notre approche de ces artefacts.
La solution la plus simple, lorsqu’un système métrologique est d’ores et déjà en place est la copie des poids un à un, de la même façon qu’exposé plus haut. Ceci dit, cette solution de facilité n’est pas toujours possible ou accessible. Cela est notamment le cas lors de la création d’un système ad hoc ou lorsque, pour une raison ou une autre, le besoin se fait sentir de créer une nouvelle fraction ou un nouveau multiple à un système déjà établi.
Dans le cas des multiples, le calcul de la masse désirée peut se faire par addition de deux poids requis, l’erreur instrumentale induite par la création des deux premiers se répercute alors sur le troisième. Cette solution est relativement aisée à mettre en œuvre mais n’est applicable que dans le cadre d’un lot de poids déjà relativement avancé, permettant de combiner plusieurs poids entre eux. Une solution commode pour les poids en métaux fusibles est l’accumulation de la matière nécessaire unité par unité en répétant l’opération de pesée autant de fois que nécessaire (peser cinq fois l’équivalent d’une unité de matière pour réaliser un multiple de cinq). Cette solution a le désavantage majeur d’être invérifiable une fois l’objet fini et il est difficile de dire à quel point elle peut être jugée acceptable par des spécialistes protohistoriques.
Ainsi, un certain nombre d’erreurs peuvent s’accumuler dès la phase de création de poids de balance, pour des raisons diverses et avec des impacts tout aussi différents. Cependant, ces déviations ont la spécificité d’être suffisamment acceptables pour ne pas entraver la fonctionnalité des instruments de pesée concernés.
2. Processus post-dépositionnels
et stabilité des matériaux
Les facteurs propres aux processus post-dépositionnels sont bien ancrés dans l’esprit collectif, qu’il s’agisse de la disparition des matériaux “périssables” ou de la patine verte des produits en alliage cuivreux. Ils font parfois même oublier que ces objets revêtaient une apparence souvent bien différente lorsqu’ils étaient utilisés. Cependant, la variation de la masse des matériaux durant leur enfouissement reste mal caractérisée. La principale raison à cela est la différence majeure d’environnements d’un site à l’autre et les différentes répercutions que cela a sur les échanges chimiques.
Nous pouvons globalement définir deux matériaux principaux qui vont entrer dans la fabrication des poids de balance : la pierre et les métaux. Bien que la catégorie des lithiques englobe plusieurs matériaux utilisés dans la confection d’artefact durant la Protohistoire (des minéraux, des roches métamorphiques, sédimentaires ou magmatiques327), nous pouvons globalement considérer que les artefacts fabriqués dans ses matériaux sont ceux souffrant le moins des affres du temps. Bien que des différences de porosité et de friabilité rendent le matériau plus ou moins résistant, il est probable que les masses actuelles des poids de balance en pierre soient sensiblement égales à celles de leur confection à partir du moment où l’objet demeure intègre.
Les métaux sont plus problématiques, la majorité d’entre eux tendent vers l’oxydation en raison de l’instabilité naturelle de cette forme. Des travaux complexes et complets ont pu être menés sur les types de corrosions affectant les métaux en fonction des différents contextes de dépôt328 et nous ne tenterons ici que de résumer l’influence possible de la dégradation du métal sur la masse des poids de balance, et comment l’appréhender dans le cadre d’une étude métrologique.
La corrosion est le résultat de processus physico-chimiques relativement complexes qui dépendent de l’objet métallique et du milieu environnant329. La corrosion par les sols, qui concerne une grande partie du matériel archéologique, se caractérise par la mise en place d’une stabilité relativement rapide qui résulte d’un équilibre matériau-milieu limitant ou stoppant la progression de la dégradation330. Cependant, la nature même du processus reste particulièrement difficile à préciser en raison du caractère unique de chaque sol et du nombre, de la complexité et de l’indépendance des paramètres rentrant en jeu331. Par conséquent, aucun modèle ne peut permettre de caractériser de manière uniforme l’impact des processus post-dépositionnels sur la masse d’un objet métallique.
La corrosion du matériel métallique est essentiellement un mécanisme d’oxydo-réduction auquel se rajoutent tous les phénomènes pouvant intervenir dans la répartition et la densité des aires anodiques et catholiques ainsi que sur l’intensité du courant entre ces aires332 dont les modes de formation peuvent amener à ralentir ou accélérer le processus de corrosion333.
Les principales conséquences de ces phénomènes sont la transformation chimique des parties corrodées, la modification de leur densité et la dégradation progressive des zones touchées. Cependant, ces éléments varient profondément d’un alliage métallique à l’autre. Ainsi, si les produits de corrosion du fer sont en général non étanches et cassables, ceux des alliages cuivreux forment bien souvent une patine étanche qui stoppe le processus. Le plomb, quant à lui, peut voir sa masse augmenter jusqu’à 25 % en raison de sa transformation en hydrocarbonates selon certains auteurs334. Pour d’autres chercheurs, il s’agit au contraire d’un matériau peu soumis aux variations à moins d’être confronté à des couches d’enfouissement d’incendie ou riches en détritus organiques335.
En l’absence d’analyse poussée, nous ne pouvons que réduire la prise en considération de ces phénomènes à un schéma basique déjà appliqué dans des études similaires336. Nous jugerons la fiabilité de la masse d’un objet métallique en alliage cuivreux en fonction de l’emprise de sa corrosion. Le matériel en fer et en plomb337 est plus problématique et doit être pris avec plus de précaution. S’il restera souvent impossible de dire si la masse actuelle de l’objet est plus élevée ou plus basse que sa masse lors de son enfouissement, une corrosion faible, n’affectant pas sa forme d’origine laisse envisager une faible variation de sa masse du fait des processus post-dépositionnels. À l’inverse, une corrosion importante laisse craindre une modification, si elle n’est pas nécessairement forte, tout du moins imprédictible. Dans le cadre de cette étude, la corrosion du mobilier du corpus est notée de 0 à 5 afin de pouvoir repérer et isoler les masses potentiellement problématiques (fig. 1-44).
À défaut de pouvoir calculer l’impact de la corrosion sur la masse d’un objet métallique, celle-ci sera donc juste décrite en considérant qu’une valeur de 0 ou 1 est négligeable, qu’entre 2 et 4, la masse est probablement modifiée et qu’on peut la juger peu fiable pour une valeur de 5. À la description de cet état de corrosion peuvent évidemment s’ajouter les potentielles interventions de nettoyage ou de restauration effectuées sur l’artefact.
3. Conservation des artefacts :
nettoyage, restauration et analyses
En plus des processus post-dépositionnels, les étapes de nettoyage ou de restauration, mais également les analyses ont un impact plus ou moins important sur la masse d’un objet.
Le nettoyage va bien évidemment diminuer la masse de l’objet sorti de fouilles, mais il est difficile de savoir exactement quelle relation celle-ci va avoir par rapport à la masse d’abandon de l’objet pour les raisons exposées plus haut concernant la corrosion. Lorsque le nettoyage se limite à un retrait des concrétions et du sédiment, la masse est théoriquement celle de l’objet abandonné plus ou moins les effets de la corrosion sur celle-ci. Cependant, dans bien des cas, le nettoyage va retirer une partie de la corrosion et donc diminuer la masse de l’objet. Parfois, un excès de zèle peut lourdement influer sur celle-ci par le retrait d’une quantité relativement importante de matière originale comme le montrent certains exemples du corpus (ex : LA-J et LA-K).
La restauration concerne ici essentiellement des cas de recollages et de colmatages. L’effet va donc être inverse avec un apport de matière pouvant modifier sensiblement la masse générale. Sauf exception, celle-ci est cependant relativement négligeable. En revanche, les recollages empêchent de distinguer si des parties manquent aux interfaces recollées et masquent ainsi la fiabilité des mesures. De la même façon, de telles lacunes invisibles vont avoir tendance à faire baisser la densité calculée pour l’objet.
Enfin, les analyses de composition nécessitent souvent un prélèvement (ex : HH-A) ou une abrasion d’une partie de la patine (ex : CR-F) qui vont faire perdre à l’objet une partie de sa matière et donc de sa masse. Bien heureusement, dans la plupart des cas, les poids de balance sont pesés avant ce type d’opération mais des exceptions existent malheureusement.
Les différents éléments vus jusque-là montrent que de nombreux facteurs vont venir influer sur la masse d’un poids de balance entre le moment de sa conception et celui de sa pesée par un archéologue. Tous ne sont malheureusement pas identifiables et mesurables, mais il est nécessaire d’en rappeler l’existence afin d’éviter de tomber sur quelque écueil interprétatif. La “masse actuelle” d’un artefact est donc le résultat d’une équation finalement assez complexe qui traduit l’accumulation d’erreurs, d’approximations, de détériorations et autres processus indépendants les uns des autres (fig. 1-45). Cependant, s’il faut en tenir compte avant de proposer un discours sur la métrologie ancienne, certaines approches permettent d’évacuer une partie des incertitudes posées par la biographie de l’objet.
On peut finalement résumer la masse actuelle d’un poids de balance à l’équation suivante :
mactuelle = midéelle ± efab ± Σerep ± Σmodif ± mpostdep ± mnett + mcolle – manalyse
Autrement dit, elle est égale à la masse idéelle plus ou moins l’erreur instrumentale et les manipulations liées à sa fabrication, plus ou moins le cumul des erreurs instrumentales propres à chaque reproduction s’il y a lieu, plus ou moins la somme des modifications ou ajustements effectués, plus ou moins l’effet des processus post-dépositionnels sur la masse, plus ou moins la masse excédentaire ou perdue après le nettoyage, plus la colle ajoutée moins la masse enlevée lors d’une analyse. Bien évidemment, certains artefacts ne sont pas concernés par certaines de ces étapes et les valeurs sont alors égales à zéro pour celles-ci. Cependant, cette équation est celle qui doit logiquement être gardée en tête à chaque confrontation avec un poids de balance archéologique dont la biographie n’est, de prime abord, pas connue dans son intégralité.
III. Restituer les artefacts,
approcher la masse réelle
Si un certain nombre de perturbations de l’information métrologique sont impossibles à résoudre, en particulier celles influant sur la matière même de l’artefact, comme les processus complexes de corrosion, les modifications de la forme de l’objet sont en revanche plus faciles à aborder dans le cadre d’une démarche scientifique. Ces transformations, volontaires ou non, peuvent avoir deux conséquences : l’ajout ou la perte de matière, parfois combinés sur le même artefact dans des cas d’ajustements de masse multiples ou complexes. L’objectif est ici d’examiner les différentes solutions qui s’offrent au chercheur afin de restituer ou d’approcher la “masse réelle” d’un artefact.
1. Les méthodes de restitution
en métrologie ancienne
La restitution est monnaie courante en archéologie, notamment dans le cadre de pratiques muséographiques. Elle vise dans de nombreux cas à donner une image de l’artefact plus proche de son contexte d’utilisation en le reconstituant pour partie ou totalité. L’objectif de ce qu’il est possible d’appeler la restitution pondérale diffère de ces considérations formelles et esthétiques. La finalité est ici d’ordre numérique et métrologique, autrement dit de retracer certaines étapes de la biographie d’un objet au travers de la variation de sa masse au cours du temps.
Les principes théoriques
Les bases théoriques qui président à ce type de restitution sont relativement simples. En considérant une masse de conception constante “mc” et une masse actuelle “ma” affectée uniquement par les évènements majeurs “e” correspondant à des masses positives ou négatives : modifications volontaires ou cassures. Nous pouvons soumettre l’équation suivante :
ma = mr + e1 + e2 … + en
Ainsi, si l’on considère un objet λ, d’une masse de conception mλr = 500 g qui subit deux modifications : la première consistant en un ajout de matière de 50 g (e1 = 50 g) puis une cassure entrainant une lacune de 300 g (e2 = – 300 g) l’équation est alors :
mλa = mλr + e1 + e2
mλa = 500 + 50 + (-300)
mλa = 500 + 50 – 300
mλa = 250
Cette équation est à la base de tous les calculs exposés par la suite ainsi que dans l’inventaire de poids en annexes. Évidemment, d’un point de vue archéologique, seule la masse actuelle est mesurable directement et il est donc nécessaire de renverser cette équation de telle sorte que :
mr = ma – e1 – e2 … – en
“Masse réelle” et calcul du volume par immersion
La méthode principale employée dans les dernières décennies pour déterminer la “masse réelle” à partir de la masse étudiable ou “masse actuelle” s’appuie sur les rapports entre masse, volume et densité. Elle repose sur calcul du volume actuel, la restitution de la forme de conception de l’artefact, le calcul du volume de conception et le calcul de la masse de conception. Elle s’appuie sur le rapport :
masse = volume x densité
Deux applications principales au champ des poids de balance sont à citer, celles de Cemal Pulak et de Barry Cunliffe.
Lors de son travail de doctorat, soutenu en 1996, visant à analyser les lots de poids de balance des épaves d’Uluburun et du Cap Gelidonya (Turquie), Cemal Pulak a proposé un certain nombre de restitutions de poids de balance cassés. Sa méthode, exposée dans l’appendice B des annexes de sa thèse, s’appuie sur la différence de poids d’un solide dans l’air et dans l’eau338.
Sa méthode consiste à peser l’objet dans l’air et dans l’eau dans un premier temps afin d’estimer sa “gravité spécifique” (specific gravity) ou “densité relative” (relative density). La partie lacunaire de l’objet est ensuite reconstituée dans de la plasticine et l’objet (l’objet original plus sa partie restituée) est repesé dans l’air et dans l’eau. La différence entre le poids dans l’air et dans l’eau après restauration correspond au volume de la pièce restaurée qui est alors multipliée par la densité relative afin d’obtenir la masse réelle339.
La densité relative correspond au ratio entre le poids d’un solide et le poids du même volume d’eau pure (20 °C et une pression atmosphérique de 1 hPa, correspondant au niveau de la mer). Autrement dit, le cuivre, par exemple, a une densité (ou gravité spécifique) de 8,96, ce qui signifie qu’à volume égal, le cuivre aura une masse et un poids 8,96 fois plus élevés que l’eau.
Ce procédé repose sur le principe d’Archimède qui énonce que tout corps plongé dans un fluide reçoit de la part de ce fluide une force de direction verticale, vers le haut (FA), dont l’intensité est égale au poids du volume de fluide déplacé (FP)équivalent donc à celui du solide immergé ; fig. 1-46).
Cette méthode permet des résultats relativement probants, mais elle présente toutefois des désavantages majeurs. Tout d’abord, elle implique l’immersion systématique dans un liquide des objets que l’on souhaite étudier. Si l’accès inconditionnel de C. Pulak au mobilier de ces deux épaves lui a permis cette approche, que ce soit avec les artefacts lithiques ou métalliques, une telle démarche est impossible dans le cadre d’une étude impliquant l’accès à des collections différentes dont les modalités de conservations sont propres à chacune. L’autre inconvénient de son travail est l’absence de documentation des restitutions elles-mêmes, rendant impossible toute discussion sur la forme proposée. Bien que son travail soit appliqué à des formes relativement homogènes et en général peu détériorées, il apparaît difficile de l’adapter à un corpus plus hétérogène.
Dans le cadre de l’étude du site de Danebury (Stockbridge, Hampshire, Angleterre,), B. Cunliffe a soumis une méthode de restitution reposant sur les mêmes principes que celle de C. Pulak mais dont les modalités diffèrent sensiblement. Les fouilles du site de Danebury ont amené à la découverte de plusieurs dizaines d’artefacts, pour la plupart lacunaires, identifiés d’un point de vue formel comme de possibles poids de balance. Afin de tester cette hypothèse B. Cunliffe et son équipe ont tenté de retrouver un maximum de leurs masses d’origine. Seuls trois poids étaient dans un état permettant d’assimiler leur masse actuelle à celle de leur conception (“masse réelle”) mais les auteurs estimaient qu’une vingtaine d’artefacts présentaient une forme suffisamment complète pour mettre en place un protocole d’estimation de leur masse d’origine340.
La méthode se base sur la même formule que celle de C. Pulak : densité = masse ÷ volume. Ici, en revanche, le choix est fait de calculer directement le volume par le procédé bien connu d’immersion et de déplacement de liquide. Il implique d’immerger le solide dans un contenant gradué et d’observer le déplacement de l’eau. La différence entre la mesure B et la mesure A correspond alors au volume du solide (fig. 1-47).
Afin d’éviter l’immersion directe d’artefacts archéologiques dans un quelconque liquide, ceux-ci sont scrupuleusement reproduits en plasticine et les mesures sont effectuées sur les copies ainsi obtenues. La masse est calculée selon la formule :
mr = Vr × d + 5 %
La marge d’erreur ajoutée a pour objectif de palier aux défauts de la mesure et à l’absence, dans la plupart des cas, de la bélière métallique341.
Cette approche a l’avantage d’être plus adaptée au mobilier archéologique que celle de C. Pulak puisqu’il n’est pas nécessaire d’immerger directement un artefact archéologique. Cela représente à la fois un avantage et un inconvénient. Dans le cadre du travail mené ici, la réalisation de copies en grand nombre aurait nécessité un accès particulièrement long aux collections afin de les réaliser. De plus, un certain nombre d’objets présente des corrosions qui se prêtent mal à la prise d’empreinte pour la réalisation d’une copie.
L’autre principal problème vient de la mesure par immersion elle-même. Les poids étudiés par l’équipe de B. Cunliffe présentent un volume compris entre 220 et 1330 ml et sont donnés avec une précision à 5 ml. Un bon container gradué de 1000 ml a aujourd’hui une graduation de 10 ml, soit 1 % du total. Cependant, les poids en question obligent à utiliser des conteneurs avec une ouverture beaucoup plus large (plus de 10 cm de diamètre pour la plupart). La conséquence va être le rapprochement des graduations sur le récipient pour une précision égale et donc une difficulté de lecture accrue. Le type de verre mesureur employé pour l’étude de Danebury n’est pas précisé, mais on peut douter qu’il possède une précision suffisamment fine pour avoir une véritable mesure à 5ml près. Il est donc plus probable que cela corresponde à une mesure entre deux graduations.
Une solution alternative, fondée sur le principe des vases communicants, qui est peut-être celle en vigueur dans l’étude des poids de Danebury, est d’utiliser deux containers différents, l’un destiné à accueillir l’objet mesuré et l’autre à lire la mesure (fig. 1-48). Une telle méthode permet de palier au problème de la taille de l’ouverture du récipient mesureur.

Les méthodes de C. Pulak et B. Cunliffe présentent des avantages et des défauts. Cependant, aucune des deux n’est applicable de manière homogène à des artefacts conservés dans plusieurs collections. De plus, l’étape incontournable que semble être la réalisation de copies peut vite s’avérer problématique (temps de réalisation, coût et stock des copies). Il a donc semblé nécessaire de chercher un procédé de mesure volumétrique alternatif.
2. La photogrammétrie et la modélisation
au service de la métrologie pondérale
Après plusieurs tests et tentatives, la numérisation 3D est apparue comme la meilleure solution en termes de mesure volumétrique. Dans le cadre de ce travail, le choix s’est plus particulièrement porté sur l’acquisition par photogrammétrie pour procéder à la numérisation tridimensionnelle des artefacts. Cette technologie s’intègre le mieux aux problématiques abordées, ainsi qu’aux contraintes et ressources de l’étude. Le protocole mis en place au départ a évolué au fur et à mesure des études et de l’amélioration des problématiques de la méthode. Pour ces raisons, le protocole présenté ci-après diffère légèrement de celui publié en 2015342.
Protocole d’acquisition et de traitement
L’acquisition et le traitement, s’ils sont séparés dans le temps, ne peuvent être abordés qu’ensemble pour présenter la méthodologie employée tant les problématiques de l’un sont liées aux contraintes de l’autre. Pour que le modèle 3D soit exploitable d’un point de vue volumétrique, il doit être à l’échelle et exempt de distorsion.
Le principe de la “photogrammétrie d’objets” implique l’obtention de prises de vue tout autour du sujet. Afin de maximiser le temps d’acquisition et de gérer de la meilleure manière la lumière et les flous focaux dans des environnements changeants (dépôts de collections, laboratoires, réserves de musées…), l’objet numérisé est ici placé sur une table tournante. L’appareil photographique, quant à lui, reste fixe sur un trépied tout au long du processus, dont seule la hauteur varie. Cependant, en faisant tourner l’objet (et non plus l’appareil photo), la lumière ne se trouve alors plus dans le même référentiel spatial que celui-ci et elle se projette donc différemment sur lui à chaque nouvelle prise de vue. Ce problème a été évacué par l’emploi d’une tente photographique accompagnée de deux lampes renvoyant une luminosité homogène sur tout l’environnement photographié.
Les photogrammétries d’artefacts s’appuient générale-ment sur un traitement cloisonné de deux parties de l’objet réunies dans une dernière opération. Si cette méthode marche relativement bien d’un point de vue visuel, elle amène à un certain “gonflement” des parties distales de chaque moitié d’objet (autrement dit, la partie centrale de l’objet lui-même).
Les différents essais effectués ont permis de fixer un protocole principal de travail auquel viennent se rajouter certaines spécificités en fonction des situations. Les photographies ont été réalisées avec un appareil photographique Canon EOS 1200D muni de deux objectifs : un EFS 18-55 mm destiné à la majorité des prises de vue et un Macro EFS 60 mm pour les artefacts les plus petits. La lumière est contrôlée par une tente photographique avec deux spots l’éclairant perpendiculairement à l’axe de prise de vue. L’objet est généralement placé sur un support de quelques centimètres de hauteur lui-même disposé sur une table tournante. L’appareil est réglé avec un ISO à 100 (afin de réduire le “bruit”), une ouverture de la focale très réduite (f14-f20) et une vitesse d’ouverture du diaphragme adaptée à la lumière pour une exposition relativement importante.
L’appareil photographique est quant à lui installé sur un trépied de table, à environ 30-40 cm du sujet, permettant la prise de vue depuis trois hauteurs différentes selon des angles correspondant environ à 30, 45 et 80° par rapport au plan de pose. Douze photographies sont réalisées pour chaque position, soit une rotation de la table de 30° entre chacune. L’opération est réalisée pour les deux “faces” de l’objet, celui-ci étant retourné une fois la première moitié des photographies réalisée, ce qui amène à produire un minimum de 72 images par artefact (fig. 1-49).
Ce protocole de base est cependant adapté et modifié en fonction des cas. Le principe de la photogrammétrie est relativement simple et permet, avec un peu de pratique, d’anticiper les situations particulières. Les poids cylindroïdes bitronconiques, par exemple, nécessitent un axe de prise de vue supplémentaire, parallèle au plan de pose. En effet, même avec un angle de seulement 30°, la moitié inférieure du profil est presque intégralement masquée (fig. 1-50-a) ce qui limite grandement le nombre de points de recollement entre les deux moitiés. D’autres objets, aux formes plus complexes, nécessitent souvent des vues de détail pour combler des lacunes visuelles (exemple fig. 1-50-b).

Le traitement informatique a été réalisé grâce au logiciel Agisoft Photoscan (devenu depuis Agisoft Metashape) selon des modalités relativement changeantes d’un cas à l’autre. Ce programme permet une certaine souplesse et action dans le traitement et le temps investi peut changer drastiquement d’un objet à l’autre. Dans la majorité des cas, le traitement des images se limite à un masquage rapide afin de faciliter le traitement. Celui-ci a pour but d’éliminer l’arrière-plan pour focaliser les calculs algorithmiques sur le sujet. Les traitements informatiques vont passer par plusieurs étapes de calcul : l’alignement des photographies, la création d’un nuage de points épars puis d’un nuage de points dense. Ce dernier sert de base à la création du modèle et nécessite généralement d’être nettoyé des points relatifs à des éléments externes à l’objet (fond, support, échelle, etc.). Les deux dernières étapes de calcul consistent à créer le maillage 3D (mesh) constitué de faces triangulaires obtenues par liaison des points, puis de le texturer (fig. 1-51).

Une dernière étape essentielle à notre propos consiste à mettre le modèle à l’échelle. Photoscan autorise à insérer dans le modèle un certain nombre de points coordonnés dans l’espace et de se servir de la distance entre deux points comme d’une échelle. Ces points peuvent être insérés depuis les images et sont ensuite replacés dans l’espace en fonction des coordonnées de chaque caméra. Chaque objet étant photographié avec une mire de cinq centimètres, c’est celle-ci qui sert de référentiel numérique. Pour plus de précision, deux échelles digitales sont utilisées, l’une de trente millimètres et l’autre de dix millimètres. La valeur adéquate leur est ensuite attribuée afin de mettre le maillage à l’échelle. Toutes les exportations effectuées par la suite (objet 3D ou orthophotographies) sont définies en fonction de cette échelle.
Précision volumétrique
En ce qui concerne ce protocole, l’aspect primant sur tous les autres est son adéquation à une démarche d’étude métrologique puisqu’il est utilisé avec pour seule fin celle d’une mesure volumétrique. Or, la photogrammétrie est rarement utilisée de la sorte et il a donc été nécessaire de mettre un tel emploi à l’épreuve.
La photogrammétrie est intrinsèquement une méthode de mesure de volume. Dans le cas présenté ici, le simple fait de restituer une forme complète en un seul calcul prouve la fiabilité de l’algorithme d’Agisoft. En effet, celui-ci reposant sur le repositionnement de caméras et de points dans l’espace, si ce géoréférencement échoue, il est impossible de restituer la moindre forme, même partielle. Or, les résultats obtenus montrent au contraire la bonne fiabilité du programme. Les modèles obtenus via la photogrammétrie et l’usage de Photoscan ne subissent vraisemblablement aucune distorsion majeure.
Deux paramètres peuvent cependant jouer sur la mesure du volume à proprement parler. Tout d’abord, cette méthode crée une surface en trois dimensions avec justesse mais peine à restituer les anfractuosités les plus fines de la matière, les perforations trop étroites ou les cavités plus ou moins internes. En somme, le logiciel n’est pas un scanner médical et ne peut percer la couche externe visible de l’objet et il se cantonne donc à restituer des données observables sur les photographies. Ainsi, une mesure par immersion dans un liquide sera théoriquement (les problèmes de graduations et de lecture abordés mis à part) plus à même d’être significative pour les objets aux surfaces les plus complexes.
L’autre facteur d’erreur peut provenir de la mise à l’échelle à proprement dite. Celle-ci reste visuelle, comme dans le cas de la mesure par immersion mais à l’avantage d’être ajustée numériquement, il est en effet possible de zoomer à souhait sur les photographies pour placer les points de repères servant à la mise à l’échelle. Ce placement est effectué manuellement sur deux photographies et restitué numériquement sur les autres avec une vérification manuelle. Autrement dit, il est possible de vérifier sur chacune des photographies de notre lot que l’échelle numérique correspond bien à l’échelle matérielle. Dans les plus mauvais cas, l’erreur relative avoisine 0,5 %. Cette valeur est plus qu’acceptable pour l’utilisation qui est faite de ces mesures.
Pour plus de fiabilité, les données de mesure ont également fait l’objet de tests de comparaison. Ces derniers consistent à mesurer le volume d’un même objet par plusieurs méthodes. Nous avons ainsi mesuré de plusieurs manière le volume d’une boule de billard (fig. 1-52), des sphères parfaites manufacturées pour faire exactement 57,2 mm de diamètre343 dans le cas d’une boule de billard américain comme celle utilisée dans cette expérience.
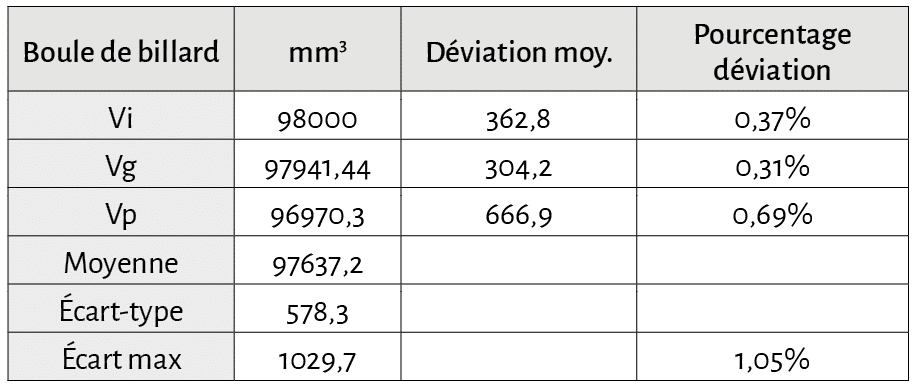
Les trois valeurs obtenues sont relativement proches, même si la sensibilité de la mesure par immersion (Vi) est plus réduite que celle des deux autres méthodes. La mesure par photogrammétrie (Vp) est celle donnant la valeur la moins élevée (96970,3 mm3) alors que la mesure par géométrie (Vg ; 97941,44 mm3) est très proche de la moyenne des mesures (97637,2 mm3). La photogrammétrie donne ainsi une mesure déviant de 0,69 % à la moyenne.
Plus récemment, une expérience d’acquisition menée dans l’UMR 5607 Ausonius a permis de comparer les volumes mesurés de 31 haches médocaines numérisées en 3D à la fois par photogrammétrie et par un scanner à lumière structurée (Artec Spyder). Les résultats montrent une déviation entre les modèles comprise entre 0 et 1,6 %.
Ces différents résultats ne permettent pas d’annoncer un chiffre tenant lieu de précision de la mesure volumétrique par photogrammétrie ; ils permettent en revanche d’en apprécier les contours. L’objectif ici n’est pas de déterminer quel degré d’exactitude la photogrammétrie apporte dans la restitution numérique d’un artefact mais d’estimer si son utilisation prend du sens dans l’étude de la métrologie pondérale ancienne.
Avantages et défauts
Le protocole d’acquisition par photogrammétrie présenté ici n’a donc pour vocation ni l’exactitude morphologique ni la perfection métrique. La démarche mise en place est un compromis réaliste présentant des avantages et des défauts.
L’utilisation de la photogrammétrie permet une réduction certaine des coûts de numérisation 3D comparé à d’autres méthodes plus performantes comme le scanner à lumière structurée. Elle permet également de réaliser l’acquisition directement dans les lieux de conservation des artefacts archéologiques avec un encombrement minium. Il s’agit également d’une opération d’acquisition relativement rapide (de cinq à vingt minutes par objet). Si la phase de traitement informatique est bien plus longue, elle ne nécessite que peu d’actions de la part de l’opérateur. Enfin, sans revenir en détail dessus, la précision atteinte est largement acceptable.
En revanche, le protocole n’est pas exempt de défauts. Il s’agit d’une méthode d’acquisition de type image-based et ne s’attache donc qu’à la surface visible des artefacts. Elle se heurte donc à des écueils lorsqu’il s’agit de restituer des parties internes ou semi-internes, telles que des dépressions profondes et/ou étroites (fig. 1-53-a), des perforations (fig. 1-53‑b) ou bien évidemment la stratigraphie interne d’un objet complexe comme les poids bimétalliques découverts dans l’épave du Bajo de la Campana (San Javier, Murcia, Espagne ; fig. 50-b). La photogrammétrie ne se fonde que sur les pixels d’une image pour en déduire sa géométrie, à l’inverse d’un scanner à lumière structurée par exemple, ce qui tend à réduire son efficacité dans certaines situations (faible luminosité, artefacts à la texture et la forme trop homogène ou d’une couleur trop sombre). Le décalage temporel entre l’acquisition photogrammétrique et son traitement informatique peut également être handicapant. Si ce dernier échoue, il n’est en effet pas toujours possible de réitérer l’acquisition. Enfin, si la précision de la restitution formelle et volumétrique est largement acceptable du point de vue des exigences de cette étude, elle n’est pas pour autant parfaite. Ainsi, le rendu restera plus précis en utilisant un scanner à lumière structurée comme l’Artec Space Spyder344.

et de perforations étroites (b).
Pour toutes les raisons exposées ci-dessus, le protocole mis en place doit être compris comme un compromis. Il ne s’agit pas de la solution parfaite mais probablement de la plus adéquate dans le cadre d’une recherche nécessitant un maximum de mobilité avec un budget réduit.
Exploitation
Le logiciel utilisé pour effectuer les travaux de modélisation est Blender (dans sa version 2.79 lors de la réalisation des modèles), un open source de modélisation et de rendu de maillages. L’étape d’exploitation des modèles 3D consiste essentiellement à reproduire numériquement ce qu’ont pu faire B. Cunliffe345 ou C. Pulak346 avec de la plasticine, à savoir reconstituer les parties manquantes d’objets cassés ou modifiés. Il peut également s’agir de l’opération inverse, autrement dit enlever numériquement une pièce ajoutée à l’objet pour l’alourdir comme les bagues de certains poids ibériques (fig. 1-54-b). Dans certains cas, il est également utilisé afin de palier à certaines insuffisances de la photogrammétrie et ainsi retravailler des modèles incomplets. Cela est notamment le cas pour un certain nombre de poids de balance ibériques, caractérisés par une perforation centrale parfois trop étroite pour être restituable.

Dans chacun de ces cas, l’opération consiste à reproduire une forme sur le logiciel qui va ensuite être ajoutée ou soustraite au modèle obtenu par photogrammétrie. Trois principaux cas de figure sont possibles : les objets cassés involontairement, ceux présentant un retrait volontaire de matière pour les alléger ou au contraire ceux auxquels a été rajoutée de la matière afin de les alourdir347.
Le cas des objets cassés est probablement celui amenant le plus de subjectivité dans le processus. En effet, les artefacts concernés présentent une lacune involontaire et aléatoire à laquelle il faut palier. Il devient donc nécessaire d’émettre une hypothèse sur la forme d’origine de l’objet à partir de la partie restante de celui-ci. Le nombre de poids de balance connus est limité et ces derniers sont assez peu normalisés dans leur forme. De plus, une erreur de restitution, si elle ne change pas drastiquement l’apparence de l’objet, peut en revanche avoir un impact important sur son volume et par conséquent la “masse réelle” qui lui sera attribuée.
Par conséquent, la justesse de la restitution sera proportionnelle au ratio entre le volume de partie conservée et le volume de la partie restaurée. Dans les cas trop sévères, où seul un fragment de poids demeure, comme certains exemplaires provenant du site de Danebury (Stockbridge, Hampshire, Angleterre), les tentatives de restitution n’ont que peu d’intérêt. En revanche lorsqu’une restitution cohérente est envisageable (généralement lorsque plus d’un tiers de l’artefact est conservé), les cas les plus complexes, dont la restitution est plus hypothétique, font l’objet de deux hypothèses : une “basse” et une “haute”. Les deux propositions correspondent à la forme la plus petite et la forme la plus grande qu’il est possible de produire à partir du fragment de départ. Deux masses sont ainsi obtenues, correspondant à deux restitutions avec des chances élevées que la “masse réelle” de l’objet se trouve entre les deux. Ce procédé est plus adéquat que l’application d’un pourcentage d’erreur car il s’appuie sur des restitutions possibles et il est donc directement dépendant de critères morphologiques observables et non métrologiques.
Les objets ayant subi un retrait volontaire de matière sont les plus faciles à traiter. Généralement, la forme d’origine est conservée dans son ensemble et seule une partie fait l’objet d’un creusement ou d’une ablation. L’opération numérique consistant à lui restituer cette partie est donc très similaire à celle des objets cassés à ceci près que la dimension subjective est beaucoup plus discrète. De plus, bien souvent, seul un pourcentage faible de la quantité totale de matière est soustrait.
Le troisième et dernier cas concerne les artefacts dont la masse a, à un moment donné, été jugée trop faible. Ils sont alors alourdis par ajout d’un matériau, le plus souvent métallique. Cette opération est la plus facile à estimer d’un point de vue formel car la place laissée à la subjectivité est, sauf exception, nulle. En effet, le matériau ajouté est généralement bien visible et appréciable d’un point de vue morphologique et peut donc être retiré aisément du modèle 3D.
Le problème posé par les objets alourdis est cependant ailleurs. La méthode de mesure volumétrique par photogrammétrie permet d’obtenir la densité moyenne d’un artefact. Cela fonctionne bien quand l’objet est fabriqué dans un seul matériau mais devient plus problématique lorsque celui est façonné à partir de deux matériaux ou plus. Sauf exception, il est impossible de déterminer la densité respective de chaque partie. Ainsi, la seule solution est de procéder au cas par cas pour proposer des “masses réelles” en fonction des densités possibles pour chaque matériau en s’appuyant sur les densités théoriques connues.
IV. Analyser la donnée métrologique
L’information métrologique doit être prise avec précaution, en tenant compte de sa biographie et des éléments qui l’impactent, mais il est également nécessaire de la traiter et de l’observer de la manière la plus objective possible. Comme nous l’avons vu, la grande majorité des études effectuées sur le territoire de l’Europe occidentale s’est concentrée sur la recherche de filiations entre systèmes métrologiques occidentaux et méditerranéens, ces derniers étant marqués par une forte diversité. À cela s’ajoute un présupposé fort, celui de l’imprécision des balances protohistoriques, qui amène à considérer des pourcentages de battement très larges (une erreur relative supérieure à 10 %).
Le problème de cette méthode est qu’elle relève d’un fort “biais de confirmation d’hypothèse”348. Cette expression est utilisée dans la littérature de psychologie pour désigner la recherche de preuves d’une manière orientée par les informations à notre disposition et nos propres expectatives. Dans le cas présent, un premier biais est fourni par l’idée non confirmée de la mauvaise précision des instruments de pesée ancien. Un deuxième biais est représenté par l’unité de comparaison choisie parmi le très large spectre des unités pondérales méditerranéennes.
Nous verrons ici les limites de la comparaison métrologique en tant que méthode d’analyse et nous présenterons le protocole retenu pour cette étude. Afin de garder un maximum d’objectivité dans l’étude métrologique, trois approches sont ici préférées à la traditionnelle recherche de correspondance avec des unités connues : l’étude des relations arithmétiques entre éléments d’un ensemble ou d’un lot ; l’analyse de la distribution des données métrologiques et l’analyse quantale ou test de Kendall.
1. Les limites de la comparaison métrologique
L’état de la recherche le montre clairement, la comparaison métrologique est, de loin, la méthode la plus utilisée en métrologie historique. De ce point de vue, considérer l’Europe occidentale durant plus d’un millénaire revient à se confronter à plusieurs dizaines d’unités pondérales qui se succèdent dans le temps ou au contraire perdurent, s’adaptent les unes aux autres et évoluent au sein de systèmes métrologiques relativement ouverts. Lorsqu’il s’agit d’étudier la métrologie protohistorique, l’hypothèse comparative renvoie systématiquement à une diffusion d’unités méditerranéennes vers l’Ouest.
Les limites de la comparaison
Même une liste non exhaustive d’unités et systèmes métrologiques employés en Méditerranée durant les âges des Métaux (voir le chapitre “Panorama des systèmes pondéraux”, p. 17) permet de comprendre les limites réelles de la métrologie comparative, qui ont déjà été fortement débattues ailleurs349, et la difficulté de l’appliquer dans le cadre de la Protohistoire occidentale.
Le graphique (fig. 1-55) représente l’emprise des systèmes métrologiques vus dans l’état de la recherche sur un intervalle entre 3 et 20 g. Il est possible de constater que la probabilité qu’une valeur ne puisse pas correspondre à un système métrologique connu par ailleurs est particulièrement faible. De plus, les intervalles sont calculés uniquement à partir des données renseignées, des diviseurs connus par l’archéologie et en prenant en compte des Normzonen à minima (+/- 2,5 % de la valeur théorique) lorsque celles-ci ne sont pas explicitement renseignées dans les publications récentes. En prenant en considération l’existence d’autres multiples et diviseurs, et/ou des Normzonen plus importantes, il est probable qu’aucune valeur n’échappe à un système métrologique ou un autre d’un point de vue théorique.

Il en va de même en considérant plus de diviseurs. En effet, il semblerait à première vue qu’aucun système connu n’englobe l’intervalle entre 6 et 6,5 g mais en réalité, il s’agit exactement du dixième de l’unité mise en évidence par K. Petruso dans l’Égéen350 dont au moins une occurrence est connue à Tylissos (Crête, Grèce)351. Ainsi, tous les intervalles vides peuvent être complétés en multipliant ou divisant l’une ou l’autre des unités par un nombre entier. Ce constat rend quasiment impossible d’infirmer une hypothèse comparative sur la base des seules données métrologiques. Cet important biais méthodologique est souvent négligé, bien qu’il soit constaté depuis certaines des études métrologiques les plus précoces352.
D’autre intervalles correspondent quant à eux à plusieurs systèmes différents qu’il est difficile pour ne pas dire impossible de distinguer sur la seule base métrologique. Cela explique notamment pourquoi il est extrêmement difficile, même en Méditerranée orientale d’attribuer un poids de balance à un système métrologique ou un autre tant les possibilités sont nombreuses. Qu’en est-il alors lorsque l’on compare entre eux des systèmes métrologiques de chronologies et d’origines différentes ?
La comparaison métrologique s’est en grande partie construite dans le cadre de la numismatique ou de la métrologie historique. La méthode repose sur l’idée que l’artefact archéologique comparé, qu’il s’agisse d’une monnaie ou d’un poids de balance, possède une masse répondant à une unité métrologique mentionnée dans les sources écrites ou épigraphiques. L’objectif principal de la métrologie historique a donc souvent été d’établir des liens entre artefacts et textes par les systèmes métrologiques identifiés. Cependant, si les textes peuvent parfois donner l’image d’une stricte normalisation de la pratique, laissant peu de place à l’innovation et à l’adaptation, l’observation du registre archéologique amène à en nuancer les résultats. Il s’agit en particulier des situations où la pratique quotidienne supplante la norme pour faciliter l’activité. Plusieurs observations susmentionnées vont dans ce sens : l’existence des mines hybrides, l’unité de conversion de 47 g, le multiple 7 du shekel de 9,3 g à Cap Gelidonya…
Dans le cas des populations protohistoriques et en l’absence de sources textuelles sur le sujet, le postulat de départ devrait être que les systèmes métrologiques utilisés ne sont pas connus. Bien évidemment, l’historiographie des dernières décennies a bien montré que cette assertion n’est que rarement prise en compte, les auteurs lui préférant généralement l’hypothèse de l’utilisation de systèmes empruntés aux populations méditerranéennes. Cependant, le nombre d’unités, et l’amplitude des intervalles de valeurs qu’elles recouvrent, rendent la comparaison particulièrement problématique. En effet, une démarche comparative permettant l’obtention d’une corrélation positive quel que soit l’élément de comparaison sélectionné n’a que peu de place dans un raisonnement scientifique. Il apparaît que la démarche est relativement absurde en cas d’absence d’indices extérieurs de l’utilisation de ces unités, non pas qu’elle ne porterait pas de résultat mais bien au contraire qu’elle validerait de manière quasi-systématique les hypothèses émises.
Pour illustrer cela, il est possible de prendre l’exemple de l’unité pondérale identifiée à Cancho Roano (Zalamea de la Serena, Badajoz, Espagne) sur la base des marques numérales inscrites sur les poids de balance (fig. 1-56). L’interprétation de M. P. García-Bellido est d’y voir l’utilisation d’un shekel syro-ougaritique de 9,4 g allégé à 9,1 g353 mais dont la matérialisation dans les lots de poids est une unité d’environ 31-36 g (autrement dit son quadruple). Or, en regardant attentivement le schéma des intervalles englobés par une unité métrologique méditerranéenne (fig. 1-55), uniquement entre 3 et 20 g, on voit qu’il est possible de formuler un nombre d’hypothèses bien plus élevé. Il peut en effet s’agir d’un quadruple de 9,1 g (9,1 x 4 = 36,4), comme c’est envisagé, mais également du quadruple d’un qedet possédant presque la même masse, de huit fois une drachme athénienne (4,35 x 8 = 34,8), de cinq fois le shekel de pesée de la laine (6,65 x 5 = 33,25), de trois fois un shekel hittite (11,75 x 3 = 35,25) ou hébreu (11,33 x 3 = 33,99). En prenant en compte des unités plus lourdes, il peut également s’agir d’une moitié d’unité égéenne (61,6 ÷ 2 = 30,8) ou encore d’un tiers de deben (93,3 ÷ 3 = 31,1).
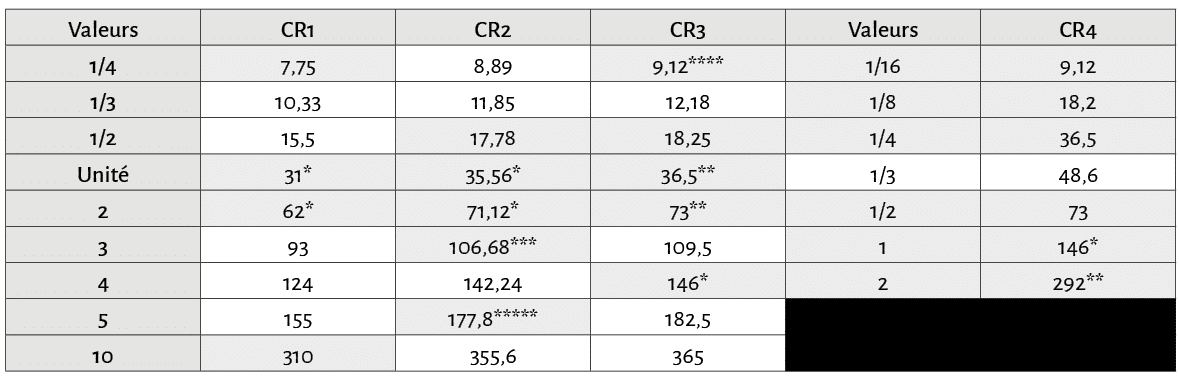
d’après García Bellido 2003, 142.
La comparaison métrologique se prête donc bien mal aux populations dépourvues d’écritures dont les seules données métrologiques directes sont les instruments de pesée eux-mêmes. La recherche en métrologie montre que dès l’âge du Bronze Méditerranéen, la pratique pondérale s’est caractérisée par la création de ponts ou de conversions entre les différentes unités et les différents systèmes métrologiques. Par conséquent, montrer un lien uniquement arithmétique entre la masse d’un poids de balance et une unité pondérale connue revient souvent à démontrer des liens arithmétiques avec la quasi-totalité des unités employées en Méditerranée, celles-ci s’inscrivant presque toutes dans un système de corrélations mathématiques volontaires.
Considérations générales
Peut-on utiliser la comparaison métrologique de manière pertinente et, si oui, comment ? La question semble légitime au regard des éléments exposés plus haut. Le risque principal de cette méthode est en effet sa faible capacité à discriminer différentes unités et par conséquent de ne jamais invalider les hypothèses émises. Il est donc certain que son usage abusif peut facilement conduire à des interprétations faussées, noyées sous des chiffres et des opérations arithmétiques qui mettent en avant les ressemblances tout en gommant les différences.
La marge de flottement qui permet de facilement glisser d’une unité à l’autre peut pourtant être pondérée par les systèmes numéraux propres à chaque unité. Malheureusement, ils sont souvent aussi nombreux et variés que les unités elles-mêmes et ne sont pas toujours d’un grand secours. Quand bien même, le simple rajout de cette nouvelle variable permet, sinon de trancher, au moins de mettre en doute l’émission de certaines hypothèses.
Pour reprendre l’exemple de Cancho Roano, qui se prête bien au jeu de la comparaison, les poids marqués comme unité (un point) pèsent 31 g, 35,56 g, 62 g, 71,12 g et 146 g. Tout pointe en direction d’un ou plusieurs systèmes métrologiques complexe à unités multiples reliées entre elles par des relations arithmétiques. Le shekel syro-ougaritique de 9,4 g, envisagé pour interpréter métrologiquement l’ensemble, est le diviseur d’une mine de 470 g, sur un système de comptage base 50. Dans le lot de Cancho Roano, les marques numérales montrent l’usage d’un système quinaire (base 5) avec des points correspondant à des multiples 1 : 2 : 3 : 5 et un diviseur par 4. L’unité la plus grosse (146 g) n’entretient pas de relation arithmétique avec la mine de 470 g ou seulement en acceptant à la fois des marges d’erreur très importantes et un système numéral distinct de celui d’origine (146 x 3 = 438). Il en va de même pour l’unité la mieux représentée (31-36 g) qui ne permet de retrouver la mine en question qu’en passant par un produit en 12,5 (36,5 x 12,5 = 456,25) et toujours en acceptant de lourdes marges d’erreurs. Ces dernières sont tellement importantes qu’il est possible d’obtenir une valeur plus proche de la mine en multipliant par 15 l’unité de CR1 (31 x 15 = 465). Comment admettre que les populations de péninsule Ibérique copient un système méditerranéen dans le cadre de pratiques commerciales si c’est pour en fournir une interprétation si libre qu’elle ne permet pas de retrouver le système métrologique original de manière intuitive ?
La comparaison métrologique ne peut avoir du sens que si elle est prise dans son ensemble et dans son contexte. Autrement dit, la comparaison n’a aucun sens si elle s’appuie sur la simple recherche de ressemblances entre unités métrologiques. En revanche, elle peut devenir intéressante lorsque le contexte archéologique permet d’ores-et-déjà de suspecter des contacts étroits entre deux zones géographiques et qu’elle s’appuie sur une vision globale de la métrologie pondérale : unités, intervalles de valeurs mesurés, systèmes numéraux employés et types d’instruments de pesée utilisés.
Pour toutes les raisons exposées, la comparaison métrologique viendra ici toujours comme dernière étape du travail d’analyse. D’un point de vue purement métrologique, elle n’interviendra qu’après l’observation par des procédés à base mathématique et uniquement lorsque d’autres éléments matériels permettront de pointer des aires géographiques susceptibles de partager les mêmes systèmes métrologiques.
2. Retrouver les relations arithmétiques
Cette première approche est à la fois intuitive et arithmétique, par sa nature, elle est celle qui se rapproche le plus des procédés amenant à la création et à l’utilisation de poids de balance. Plutôt que réellement chercher à faire ressortir une unité, l’objectif ici est de mettre en avant les relations arithmétiques reliant les poids les uns aux autres dans un ensemble d’artefacts donné.
Les lots et ensembles de poids de balance
Les relations arithmétiques qui lient les masses de poids de balances entre elles sont généralement simples : le poids “B” est égal au double du poids “A”, le poids “C” est égal à la moitié du poids “A”. Ces relations n’ont cependant de sens qu’à l’intérieur d’un ensemble de poids de balance destinés à fonctionner ensemble. Archéologiquement, cela correspond à des objets dont le contexte de découverte permet de soupçonner une utilisation conjointe, au moins dans leur dernier état de fonctionnement.
Dans cette étude, il est possible d’identifier plusieurs situations laissant envisager une utilisation conjointe d’instruments de pesée. R. Vilaça a montré que les critères typologiques n’entrent pas nécessairement en ligne de compte dans la constitution d’un set de poids de balance354, tout comme le suggèrent également les découvertes de Migennes “Le Petit Moulin” (Yonne, France)355 ou d’Étigny “Le Brassot” (Yonne, France)356. Par conséquent, seules les données stratigraphiques servent ici à émettre l’hypothèse d’une association volontaire d’objets ou non.
Deux situations sont distinguées et différenciées par les termes employés pour les définir. Le premier cas concerne les instruments dont l’association est interprétée comme volontaire et, de ce fait, peuvent être envisagés comme un lot d’instruments destinés, au moins au moment de leur ensevelissement, à une utilisation conjointe. Le terme “lot” sera donc employé pour désigner des instruments dont le fonctionnement conjoint fait peu de doute et concernera donc essentiellement les groupes de poids et éléments de balances déposés au sein d’une même tombe ou d’un même dépôt non funéraire. À cela, se rajoutent quelques cas spécifiques dont l’association est attestée par un ensevelissement rapide non volontaire, comme par exemple le lot de poids de La Hoya (Guardia, Araba, Espagne), fossilisé sur place en position de rangement par un incendie357.
Au terme de “lot” est préféré celui “d’ensemble” pour parler d’instruments trouvés dans un contexte stratigraphique similaire mais non clos. Cela est notamment le cas lorsque des objets sont retrouvés dans une même unité stratigraphique ou une même structure mais sans que la taphonomie ne permette d’assurer une association directe. Dans ces cas-là, leur utilisation conjointe est fortement envisageable et amène, pour cette raison à les réunir, tout en maintenant une distinction avec les lots dont le caractère unitaire est plus prononcé.
En d’autres termes, les lots sont des ensembles dont l’utilisation conjointe est assurée alors que les ensembles sont de potentiels lots dont l’utilisation conjointe est donnée comme hypothèse.
Dans les cas des lots comme des ensembles, l’hypothèse de départ est que les poids les constituant ont de fortes chances de fonctionner comme un tout cohérent et ainsi présenter des relations arithmétiques relativement lisibles. Pour cette raison, ils peuvent être analysés différemment des plus grandes séries.
La table de division
Le principe de la “table de division” est de mettre en évidence les relations arithmétiques entre les différents poids d’un lot ou d’un ensemble. Ce procédé a été utilisé pour la première fois avec le lot de dix poids de la tombe 200 d’El Cigarralejo (Mula, Murcia, Espagne) dans le cadre d’un mémoire de Master en 2013358 puis développé dans un article en 2015359.
Un lot de poids de balance peut être caractérisé comme le regroupement d’une unité et/ou360 de ces multiples et/ou de ces fractions. Autrement dit, on peut le définir comme :
x1 × U + x2 × U … + xn × U
avec “U” représentant l’unité du système métrologique et “x” une valeur fraction ou multiple du système de comptage avec un ratio de x1 : x2 : … : xn.
Dans l’introduction de son article sur la recherche des “plus anciens poids”, L. Rahmstorf expose une liste de critères permettant l’identification des poids de balance, notamment la lecture intuitive du système métrologique sous-jacent qui doit former une “séquence logique”361. L’objectif ici est de rendre ce système encore plus lisible en le réduisant à cette seule séquence logique.
Cela a été dit, un système métrologique est composé de diviseurs, exprimés sous forme décimale ou de fraction, et de multiples exprimés sous la forme de nombre entiers. Ce sont ces multiples qui vont permettre l’identification par la table de division. La formule exposée un peu plus haut permet d’admettre que toutes les masses des poids d’un lot sont exprimable sous la forme d’un multiple ou d’une fraction de l’unité. Par conséquence, en divisant chacune de ces masses par l’unité en question, le résultat égalera le multiple ou la fraction correspondant et il est ainsi possible de réduire la liste des valeurs absolues en gramme à une liste de relations arithmétiques correspondante aux ratios entre chaque masse sous la forme :
x1 + x2 … + xn
Cette opération est cependant irréalisable dans notre cas puisque l’objectif est justement la recherche de l’unité “U”. Cependant, il est possible de poser l’hypothèse de départ qu’au moins un des poids du lot ou de l’ensemble correspond à l’unité recherchée. L’objectif du tableau de division est d’expérimenter chaque masse des poids d’un lot comme une unité hypothétique en réalisant l’opération exprimée plus haut.
Autrement dit, un tableau est dressé avec les dividendes sur la première colonne et les diviseurs sur la première ligne (fig. 1-57).
Chaque cellule de ce tableau présente les quotients des opérations effectuées, autrement dit, la séquence arithmétique liant la masse concernée à celle de toutes les autres du lot est lisible dans chaque colonne. Il est ainsi possible de déterminer la séquence la plus à même d’être la bonne ainsi que le poids le plus susceptible de correspondre à l’unité.
Afin d’illustrer cela, il est possible de présenter l’exemple de la tombe 200 d’El Cigarralejo qui a servi de galop d’essai à ce procédé. Ce lot de dix poids de balance, qui sera analysé plus en détail dans la partie sur les instruments de pesée du Second âge du Fer, a été trouvé dans une sépulture à crémation et laisse peu de doute quant à l’usage conjoint des poids qui le composent, au moins au moment du dépôt funéraire. Pour des raisons de clarté, les dénominations proposées lors de l’article de 2015 (de I à X)362 sont remplacées ici par les désignations du corpus exposées en Partie 3 soit de Cig-A à Cig-L. Les poids présentent une masse graduelle de 1,98 g à 208,45 g et ont été analysés métrologiquement par le biais de la table de division suivante (fig. 1-58).
Le premier résultat est qu’une séquence logique apparaît clairement et permet de rejeter complètement l’hypothèse de l’absence de construction pondérale tout comme celle d’une série de poids qui n’aurait pas destination à fonctionner ensemble. En effet, en l’absence de construction pondérale volontaire, ce type de table de division montrera des multiples entiers mais non consécutifs ou avec des erreurs relatives inconstantes. Ici, certaines relations arithmétiques sont sans équivoque : Cig-200-H (81,65 g) est le double de Cig-200-G (41,46 g) qui est le double de Cig-200-F (20,48 g). Quant à la recherche d’une unité dans ce lot, on peut voir que peu de poids testés présentent des multiples entiers. L’existence de ces derniers ne peut jamais être un critère décisif, on remarque toutefois que la création de multiples décimaux n’a que peu d’intérêt et de logique lorsque des poids correspondent aux fractions, sauf dans le cas de constructions complexes. Ainsi, seuls les poids Cig-200-F (20,48 g) et Cig-200-G (41,46 g) offrent des multiples cohérents, respectivement
2 : 4 : 6 : 10 et 2 : 3 : 5 (fig. 1-58 partie grisée). Du point de vue des seuls résultats du tableau de division, ces deux poids sont de bons candidats à la fonction d’unité du lot. Dans ce cas précis, d’autres éléments exposés en 2015363 et réexpliqués dans la partie correspondante permettent de considérer le poids Cig-200-F comme le plus probable des deux.
Considérations générales
L’analyse métrologique des lots et ensembles de poids de balance par le biais des tableaux de division a donc avant tout pour objectif de mettre en avant leurs relations arithmétiques. Les informations qu’il est possible d’en tirer dépendent ensuite de la construction du lot et des informations contextuelles et comparatives à disposition.
L’une des principales limites de cette méthode est qu’elle se focalise sur la mise en évidence de multiples entiers. Or, certains systèmes recourent possiblement à l’utilisation de multiples décimaux (non entiers) alors que d’autres privilégient les fractions comme les systèmes orientaux basés sur la division d’une mine. Enfin, sans que cela ne soit un obstacle insurmontable, les systèmes complexes sont plus difficiles à caractériser par cette méthode. On peut considérer comme complexe un système ayant recours à plusieurs unités différentes, chacune étant égale à un multiple de l’autre. Le système métrique en est un puisque l’unité change à chaque palier de dix : 10 mètres égalent 1 décamètre, 10 décamètres égalent 1 hectomètre, 10 hectomètres égalent 1 kilomètre etc… Dans le cas du système métrique, la régularité même de sa structure fait qu’il est aisément identifiable, peu importe l’unité prise en compte. En revanche, lorsqu’ils sont moins réguliers, ces systèmes peuvent poser problème. C’est par exemple le cas du système pondéral grec basé sur un talent équivalent à 60 mines, une mine égale à 100 drachmes et une drachme valant 6 oboles. Cette succession d’unités dont les relations arithmétiques changent rend sa caractérisation ardue sur de simples bases mathématiques, d’autant plus que le système de comptage est à la fois décimal et sexagésimal.
La méthode d’analyse intuitive et arithmétique n’est donc pas adaptée à toutes les situations et c’est pour cela qu’il est nécessaire de la coupler à d’autres procédés.
3. L’analyse de la fréquence de la distribution
La distribution des données représente un indice primordial pour déterminer la nature d’un échantillon. Ainsi, dans le cas d’une répartition dite normale ou gaussienne, le plus grand nombre d’individus approchera une valeur moyenne tandis que le nombre d’individus diminuera en s’éloignant de celle-ci.
L’analyse d’une distribution ne prend de sens que dans le cas d’un échantillon relativement important et se différencie donc de la table de division, plus à même de servir à l’étude des échantillons réduits mais au fonctionnellement cohérent. À l’inverse d’une répartition normale, une “répartition métrologique” se caractérise par un nombre d’individus élevés autour de plusieurs valeurs cibles qui entretiennent entre elles des rapports arithmétiques : l’unité, certaines de ses fractions et certains de ses multiples. Dans le cas d’une répartition métrologique parfaite, l’échantillon devrait présenter des individus correspondant exactement à ces valeurs et aucun individu entre celles-ci. La réalité est évidemment plus complexe puisque nous devons compter avec une Normzone, ce qui nous amène donc à caractériser la répartition métrologique comme une addition de répartitions normales autour de plusieurs valeurs cibles arithmétiquement liées.
Plusieurs méthodes existent pour analyser une fréquence de distribution mais nous proposons ici une manière de l’aborder en prenant en compte une Normzone déterminée par l’opérateur et modifiable. L’objectif de l’analyse de la distribution est en effet ici de déterminer les éléments de l’échantillon qui peuvent correspondre à une même valeur. En choisissant des intervalles arbitraires, nous risquons de diviser l’échantillon. Si nous prenons l’exemple d’un échantillon structuré par une unité de 101 g (information recherchée et qui n’est donc pas à notre disposition) et que nous déterminons des intervalles d’observation de 5 g, l’analyse donnera un nombre d’individu entre 95 et 100 g et un autre résultat entre 100 g et 105 g. Ainsi, des éléments de 99 g (qui présentent donc une déviation à la norme de moins de 2 %) apparaîtront dans le premier intervalle alors que ceux correspondant exactement à l’unité seront dans le second avec des éléments allant jusqu’à 105 g (soit une déviation d’environ 4 %).
Pour remédier à ce problème, nous proposons une méthode fondée sur le choix de plusieurs critères : un intervalle de recherche, un incrément et une Normzone (exprimée en pourcentage).L’intervalle de recherche est l’emprise de la recherche tandis que l’incrément correspond à la “résolution” d’observation.
Dans un intervalle [1 : 10 g], par exemple, avec un incrément de 0,1 g, le comptage va être effectué à partir des valeurs {1 g, 1,1 g, 1,2 g […] 9,9 g et 10 g}. La Normzone va ici déterminer chaque intervalle de comptage. Si nous reprenons le cas précédent, pour une Normzone de 5 %, nous déterminons, pour chaque valeur testée, un intervalle égal à [valeur testée – 5 % : valeur testée + 5 %]. L’amplitude de l’intervalle dépend donc de la valeur testée. Pour la valeur 1 g, l’intervalle correspondre à [0,95 : 1,05 g] alors qu’il équivaudra à [9,5 : 10,5 g] pour la valeur 10 g (fig. 1-59). Une telle procédure peut par conséquent amener à compter une même valeur dans plusieurs intervalles différents mais elle permet de s’affranchir des possibles fluctuations dues aux erreurs et imprécisions en donnant le nombre maximum d’individus pouvant correspondre à une valeur en admettant une Normzone donnée.

4. Les statistiques appliquées à la métrologie
Les instruments de pesée découverts associés dans des contextes clos sont rares et l’étude de larges séries, pouvant couvrir des zones étendues et des périodes de temps relativement longues, est un passage obligé. L’avantage des statistiques est de pouvoir traiter une quantité élevée de données regroupées selon des critères choisis en amont.
Cependant, les systèmes métrologiques ont des caractéristiques numériques relativement particulières puisqu’ils résultent d’une opération volontaire de normalisation selon plusieurs valeurs (unités, fractions et multiples). Cette partie a pour objectif de proposer une présentation rapide des différentes solutions mathématiques et statistiques applicables aux considérations métrologiques.
Le problème posé par les systèmes métrologiques et les instruments qui servent à les appliquer est leur construction volontairement mathématique. Pour cette raison, la plupart des tests habituellement utilisables, en particulier ceux basés sur la répartition normale d’un échantillon, sont ici inutiles. Heureusement, plusieurs spécialistes se sont penchés sur la question et ont réussi à mettre en place des protocoles d’analyse spécifiques à la métrologie.
Le Cosine Quantogram Analysis de Kendall
“There are two reasons why technical jargon is out of place on an occasion such as this. In the first place, those to whom it is unfamiliar may lose the thread of the argument, while secondly […] others to whom it is only marginally familiar may be tempted to give to the argument greater weight than it deserves, for no better reason than that it is seductively incomprehensible.”
(D. G. Kendall, Hunting quanta, 1974, p. 231)
L’analyse du Cosine Quantogram (CQA) a été sinon théorisée au moins mise en forme de manière éloquente et relativement intuitive par D. G. Kendall en 1974364 (au point de devenir éponyme). Son propos étant complet, abordable et résolument tourné vers l’archéologie, il serait malavisé de tenter d’en résumer les tenants et aboutissants. Aussi vais-je me conformer à la recommandation qu’il se prescrit à lui-même dans son introduction, citée ci-dessus, en évitant de rentrer dans les détails techniques d’une telle méthode pour me contenter d’en expliquer les objectifs et les clés de lecture.
D. G. Kendall définit le CQA à partir des travaux pionniers de Thom et surtout Broadbent365 avec pour objectif de le rendre à la fois adapté à l’analyse d’un grand nombre de données et indépendant de critères subjectifs366. Elle repose sur la recherche dans un échantillon d’un quantum, défini par Thom et Broadbent367, autrement dit l’unité autour de laquelle sont arithmétiquement échelonnées les mesures de l’échantillon.
D. G. Kendall définit la formule suivante :
Où ∅(τ) est un taux pour une population testée de taille N dépendant de la taille de celle-ci par l’expression 2/N; Xj est une observation unique (autrement dit chaque mesure effectuée et testée) ; et τ est l’inverse du quantum testé (i.e. 1/q) ; enfin, 2πXj τ représente l’erreur exprimée en valeurs angulaires368. Dans le cas d’une population non quantale dont la taille est suffisamment importante et dont les valeurs de q ne sont pas trop grandes, ∅(τ) est très proche d’une valeur aléatoire d’une gaussienne. D. G. Kendall a calculé que la probabilité que ∅(τ) excède +4 pour une population non quantale avoisine les 0,000032369.
La procédure d’utilisation du CQA est relativement simple. Plusieurs valeurs de q sont testées et les valeurs les plus hautes de ∅(τ) correspondent aux quanta les plus probables pour l’échantillon. Les résultats sont généralement visualisés à l’aide d’un graphe où ces derniers correspondent aux pics positifs de la courbe (fig. 1-60).

Pour illustrer cela, prenons l’exemple d’un échantillon artificiel construit sur la base d’un système numéral quinaire/décimal (bases de comptage 5 et 10), d’unité 1, dont les multiples théoriques sont indiqués dans la deuxième colonne du tableau (fig. 1-60). Pour chacun de ces multiples est mesurée une masse correspondant à ce multiple +/- une erreur. Ici, ces valeurs sont obtenues par une formule aléatoire370 correspondant au multiple en question plus ou moins une erreur relative de 5 %. On peut voir sur la visualisation des résultats trois pics principaux correspondant à 5 ; 25,2 et 52,4 g, autrement dit, les unités structurantes de l’échantillon testé, et non pas l’unité réelle qui est égale à 1.
Comme le dit très justement D. G. Kendall, il ne faut cependant pas donner aux chiffres et aux résultats de cette méthode plus de poids qu’ils n’en ont. En effet, dans l’exemple créé artificiellement pour illustrer la méthode, le système serait considéré par ses utilisateurs comme ayant une base décimale. Pourtant, les résultats de l’analyse favorisent l’interprétation d’une base quinaire en raison des subdivisions du système décimal.
Par conséquent, l’analyse du CQA de D. G. Kendall est un outil puissant qui permet de rapidement mettre en évidence des unités structurantes dans un jeu de données. Comme vu précédemment (voir “Christopher Pare : la première synthèse”, p. 35), il a été fortement utilisé et révisé au cours des dernières années dans les discussions sur la métrologie371. Dans les annexes de son étude sur les poids d’Ayia Irini, K. Petruso a pu tester la capacité de l’analyse de Kendall à isoler, avec un degré de confiance élevé, plusieurs quanta dans un échantillon372. Il nécessite cependant une comparaison avec la donnée originale (les valeurs de notre échantillon) afin de vérifier la cohérence matérielle des résultats qu’il apporte. En effet, si dans notre exemple, deux pics de hauteurs similaires correspondent respectivement à 10,1 g et 12,5 g, ce dernier n’a pas de sens réel dans l’échantillon mais résulte de la proximité mathématique entre le double de notre multiple 6 (représenté dans l’échantillon par la valeur 6,26 g) et la moitié du multiple 25 (représenté par les valeurs 24,75 g et 24,22 g) égale à 12,5.
Considérations générales
Les approches non-inductives et tout particulièrement l’analyse du Cosine Quantogram sont d’une grande aide lorsqu’il s’agit de rechercher de possibles unités dans un échantillon de grande taille et la capacité de cette dernière à mettre en évidence plusieurs quanta a pu être mise en évidence373. De plus, la visualisation sous formes de graphes permet la juxtaposition rapide de plusieurs résultats afin de comparer aisément des échantillons différents tout en se détachant mentalement des chiffres qui peuvent facilement induire en erreur.
Aujourd’hui encore, la métrologie historique et archéologique se passe grandement de tels outils pour construire des hypothèses, probablement par méconnaissance ou manque de lisibilité des méthodes. Par exemple, le thème de la normalisation pondérale du métal (sous la forme d’objets entiers ou fragmentés) dans une optique prémonétaire, malgré l’intérêt des hypothèses émises, ne fait presque jamais intervenir de démarche mathématique ou statistique dans l’analyse374.
La démocratisation de la méthode ne doit cependant pas entraîner une baisse du rétro-contrôle de la donnée et amener à masquer le raisonnement par des jeux de chiffres et de graphiques. Comme cela a déjà été mentionné, l’analyse du CQA va mettre en évidence une unité structurante sur une base mathématique et, par conséquent, indépendamment des conditions qui président à sa construction. De plus, à la différence d’autres tests mathématiques, le résultat ne peut être corroboré directement par un test de signifiance, celui-ci étant proportionnel à la taille et à la construction de l’échantillon. Il peut donc être facile de se fourvoyer en accordant trop de confiance à un résultat, en particulier lorsque l’échantillon est de taille réduite375.
Enfin, même lorsqu’un quantum avéré est détecté, il reste le résultat d’une opération mathématique propre à l’échantillon testé. Comme dans le cas de notre échantillon artificiel, les valeurs les plus hautes de ∅(τ) ne correspondent pas nécessairement à l’unité qui sert de base à la création théorique du système métrologique mais à celle structurant “le mieux” l’échantillon.
5. Metrological ToolBox :
une boîte à outils pour l’analyse métrologique
Afin de faciliter la mise en œuvre des analyses métrologiques exposées ci-dessus, dans le cadre de cette étude mais surtout dans l’idée de l’exportation du protocole pour d’autres travaux, un support informatique a été créé. Celui-ci vise à supporter les trois analyses décrites à l’aide d’un tableur automatisé. Deux versions en existent, l’une utilisable sur le logiciel privé Microsoft Excel et l’autre sur le logiciel libre de droit LibreOffice/OpenOffice Calc. Cet outil est mis à disposition de la communauté scientifique dans l’espoir de multiplier les analyses métrologiques de données archéologiques fondées sur un protocole cohérent.
MetroTB repose sur l’utilisation de trois feuilles correspondant aux trois analyses (plus une feuille dédiée à l’insertion des données brutes) : la table de division avec l’outil TabDiv ; l’analyse quantale via l’outil CQA et l’analyse de distribution avec HistoVal376.
Il est à noter que les versions Excel et LibreOffice varient sensiblement, notamment dans l’exportation graphique des résultats, et que les données qui seront présentées ici reposent sur l’usage de la version Excel.
Notes
- Voir notamment : Gossellin 1822 ; Mongez 1831 ; Böckh 1838 ; Vázquez Queipo 1859 ; Madden 1864 ; Brandis 1866 ; Murray 1868 ; Dumont 1869 ; Schillbach 1877 ; Chabas 1878 ; Pernice 1894 ; Rouvier 1897 ; Germer-Durand 1898 ; Clermont-Ganneau 1898 ; Enjoy 1900 ; pour une bibliographie plus complète, voir : https://pondera.incal.ucl.ac.be/bibliography/.
- Voir par exemple : Garnier et al., éd. 1989 ; Petruso 1992, 44 ; Ascalone & Peyronel 2006, 18‑20.
- Kula 1977, 481‑483.
- Böckh 1828.
- Böckh 1838.
- Böckh 1838, 32‑45.
- Pour une critique de l’approche comparative voir : Ascalone & Peyronel 2006, 18‑20.
- Hultsch 1864 ; Hultsch 1882 ; Hultsch 1898.
- Lehmann-Haupt 1889a ; Lehmann-Haupt 1889b ; Lehmann-Haupt 1893 ; Lehmann-Haupt 1895 ; Lehmann-Haupt 1909 ; Lehmann-Haupt 1912 ; Lehmann-Haupt 1918.
- Ridgeway 1887 ; Ridgeway 1889 ; Ridgeway 1892.
- Viedebantt 1917 ; Viedebantt 1923.
- Petrie 1926.
- Voir par exemple : Thureau-Dangin 1909 ; Thureau-Dangin 1921 ; Thureau-Dangin 1927 ; Belaiew 1929 ; Belaiew 1934 ; Hemmy 1935 ; Hemmy 1937.
- Kula 1977, 481‑483.
- Parise 1970 ; Parise 1971 ; Parise 1981 ; Parise 1984.
- Zaccagnini 1979 ; Zaccagnini 1986 ; Zaccagnini 1999 ; Zaccagnini 2000.
- Liverani 1972.
- Ascalone & Peyronel 2006, 23‑24.
- Schliemann 1879 ; Evans 1906 ; Petrie 1926.
- Petruso 1992.
- Petruso 1978.
- Pulak 1996. Remarque : la thèse en question n’a jamais fait l’objet d’une publication intégrale mais a été mise à disposition en ligne dans sa version de soutenance. La pagination s’appuie donc sur cette version.
- Kendall 1974.
- Alberti et al. 2006, 1.
- Ascalone & Peyronel 2006, 20.
- Buchez 2010.
- Lassen 2000, 233.
- Petruso 1981, 45‑47 ; Lassen 2000, 233.
- Lassen 2000, 233.
- Lassen 2000, 234.
- Petruso 1981, 45.
- Lassen 2000, 234.
- Ascalone & Peyronel 2006.
- Voir notamment Parise 1970 ; Parise 1981 ; Parise 1984.
- Ascalone & Peyronel 2006, 23.
- Ascalone & Peyronel 2006, 25‑26 ; Rahmstorf 2006, 32.
- Ascalone & Peyronel 2006, 25‑26 ; Finkielsztejn 2015, 175.
- Ascalone & Peyronel 2006, 26.
- Ascalone & Peyronel 2006, 27.
- Petruso 1992, 26‑34.
- Ascalone & Peyronel 2006, 28.
- Zaccagnini 1999 ; Ascalone & Peyronel 2006, 29.
- Ascalone & Peyronel 2006, 39.
- Ascalone & Peyronel 2006, 30‑40.
- Ascalone & Peyronel 2006, 40‑49.
- Rahmstorf 2010, 98.
- Rahmstorf 2010, 98.
- Idem.
- Pulak 1996, 279‑281.
- Parise 1993 ; Parise 1997.
- Zaccagnini 1991.
- Elayi & Elayi 1997, 319‑320.
- Kroll 2008 ; van Wees 2013, 110.
- Van Wees 2013, 110.
- Van Wees 2013, 110‑111.
- Meadows & Shipton 2001, 17.
- Van Wees 2013, 110.
- Osborne 1996, 253‑255.
- Osborne 1996, 251.
- Seaford 2004, 138‑139 ; Graeber 2016, 299‑300.
- Meadows & Shipton 2001, 18.
- Van Wees 2013, 108‑109.
- Meadows & Shipton 2001, 18.
- Van Wees 2013, 107.
- Meadows & Shipton 2001, 18.
- Van Wees 2013, 116.
- Harding 1994, 129‑132 ; van Wees 2013, 115‑118.
- Van Driessche 2009, 71‑74.
- Van Driessche 2009, 93‑94 ; Doyen 2016, 84.
- Van Wees 2013, 108‑109.
- Finkielsztejn 2015, 179.
- Ripollès 2005, 187 ; Ripollès 2013, 6‑7.
- Richard & Villaronga 1973, 103 ; Alexandropoulos 1987, 12.
- Richard & Villaronga 1973, 104 ; García Bellido 2013, 41.
- Nieto-Pelletier 2012, 237‑238.
- Hiriart 2016, 153.
- Richard & Villaronga 1973, 94.
- Ripollès 2005, 189 ; Ripollès 2013, 13.
- Richard & Villaronga 1973, 96‑97.
- Richard & Villaronga 1973, 98.
- Richard & Villaronga 1973, 99.
- Richard & Villaronga 1973, 103‑105.
- Richard & Villaronga 1973, 128.
- Richard & Villaronga 1973, 129‑131.
- Gorgues 2010, 215‑220 ; Gruel 2012 ; Callegarin & Hiriart 2013, 12 ; Callegarin et al. 2013, 185‑190.
- Gross 1883, 51 ; Gross 1883, fig. 7.
- Boissinot 2010, 333‑342.
- Forrer 1906, 1.
- Forrer 1906, 57.
- Forrer 1906, 39‑54.
- Forrer 1923, 91‑94.
- Forrer 1923, 93.
- Philippe 1937, 296‑297.
- Galilea Martínez 2004, 242 ; Michailidou 2005, 15 ; Calvo García 2006, 36 ; Ripollès 2011, 219.
- Desor 1870a ; Desor 1870b.
- Morel Fatio 1886.
- Pilloy 1888, 125.
- Blanchet 1890.
- Blanchet 1905, 21‑29.
- Gérin-Ricard (de) 1901.
- Déchelette 1910.
- Déchelette 1914.
- Déchelette 1910, 401-402 ; 406 ; Déchelette 1913, 799.
- Déchelette 1910, 400.
- Déchelette 1910, 397‑406.
- Déchelette 1910, 407.
- Déchelette 1914, 1557‑1558.
- Böckh 1838.
- Hultsch 1882 ; Hultsch 1898.
- Déchelette 1910, 402.
- Déchelette 1910, 405.
- Bénard le Pontois 1929.
- Smith 1905.
- Allen 1968, 321.
- Briard & Rivalain 1987 ; Briard 1987b ; Briard 1994 ; Briard 2001.
- Briard 1987b, 731 ; Briard 1987a, 138.
- Louis et al. 1955, 193‑202.
- Guilaine 1969 ; Guilaine 1970 ; Guilaine 1972 ; Guilaine et al. 2017.
- Spratling 1980.
- Lenerz-de Wilde 1995 ; Pare 1999, 478 ; Lenerz-de Wilde 2002 ; Pare 2013, 513.
- Peroni 1998, 221‑222.
- Primas & Della Casa 1996, 84, 156.
- Eiwanger 1989, 459‑461.
- Primas 1986, 38‑41.
- Primas 1997, 123‑124.
- Ruiz-Gálvez Priego 2003, 149.
- Malmer 1989 ; Malmer 1992 ; Sperber 1993.
- Eiwanger 1989.
- Ruiz-Gálvez Priego 2000, 267‑268.
- Ruiz-Gálvez Priego 2000, 268.
- Zaccagnini 1991.
- Galán Domingo & Ruiz-Gálvez Priego 1996, 153‑156 ; Ruiz-Gálvez Priego 2000, 269‑272.
- Northover 1989, 125‑126.
- Zaccagnini 1991, 344 ; Ruiz-Gálvez Priego 2000, 272.
- Armbruster 1996.
- Ruiz-Gálvez Priego 2000, 275.
- Bénard le Pontois 1929.
- Briard 1987a, 134.
- Gross 1883.
- Forrer 1923.
- Malmer 1992.
- Lenerz-de Wilde 1995.
- Cardarelli et al. 1997 ; Cardarelli et al. 2001.
- Pare 1999 ; Pare 2013.
- Peake et al. 1999 ; Peake & Séguier 2000.
- Cardarelli et al. 1997 ; Cardarelli et al. 2001, 38.
- Cardarelli et al. 1997, 630.
- Cardarelli et al. 1997, 632.
- Cardarelli et al. 1997, fig. 361‑362.
- Cardarelli et al. 1997, 632‑635 ; Cardarelli et al. 2001, 41.
- Cardarelli et al. 1997, 636‑638 ; Cardarelli et al. 2001, 38‑41.
- Cardarelli et al. 2001, 37‑41.
- Petruso 1978 ; Petruso 1992.
- Cardarelli et al. 2001, 41.
- Pare 1999.
- Pare 1999, 422‑454.
- Pare 1999, 455‑464.
- Pare 1999, 464‑467.
- Pare 1999, 476.
- Pare 1999, 488.
- Lenerz-de Wilde 1995.
- Primas 1997 ; Primas & Pernicka 1998.
- Petruso 1978 ; Petruso 1992.
- Pare 1999, 505‑506.
- Pare 1999, 510.
- Peake et al. 1999.
- Peake & Séguier 2000.
- Gomez de Soto 1996.
- Peake et al. 1999, 644 ; Peake & Séguier 2000, 27.
- Rahmstorf & Pare 2007.
- Pare 1999.
- Rahmstorf 2003 ; Rahmstorf 2006 ; Rahmstorf 2010.
- Rahmstorf & Pare 2007, 268‑270.
- Cardarelli et al. 1997 ; Cardarelli et al. 2001.
- Rahmstorf & Pare 2007, tableau 1.
- Rahmstorf & Pare 2007, 281.
- Rahmstorf 2014.
- Rahmstorf 2014, 112‑114.
- Rahmstorf 2014, 117‑118.
- Rahmstorf 2018 ; Rahmstorf 2019 ; Ialongo & Rahmstorf 2019 ; Hermann et al. 2020.
- Muller 2007a ; Muller 2007b.
- Roscio 2007.
- Roscio et al. 2011.
- Roscio 2018a.
- Kendall 1974.
- Ballester Tormo 1930.
- Ballester Tormo 1930, 1‑2.
- Ballester Tormo 1930, 4.
- Ballester Tormo 1930, 4‑5.
- Ballester Tormo 1930, 16.
- Ballester Tormo 1930, 12, 21‑22.
- Ballester Tormo 1930, 18‑19.
- Ballester Tormo 1930, 20.
- Ballester Tormo 1930, 22.
- Beltrán Villagrasa 1948.
- Beltrán Villagrasa 1948, 131.
- Lehmann-Haupt 1889a, 254 ; Lehmann-Haupt 1931.
- Beltrán Villagrasa 1948, 134‑135.
- Beltrán Villagrasa 1948, 136‑137.
- Cuadrado Díaz 1964.
- Cuadrado Díaz 1964, 347.
- Cuadrado Díaz 1964, 348.
- Fletcher Valls & Mata Parreño 1981.
- Fletcher Valls & Mata Parreño 1981, 166.
- Fletcher Valls & Mata Parreño 1981, 167.
- Lazaro Mengod et al. 1981, 175.
- Pellicer i Bru 1985.
- Richard & Villaronga 1973, 127 ; Fletcher Valls & Silgo Gauche 1995, 275.
- Oroz Arizcuren 1979b.
- Oroz Arizcuren 1979b, 289 ; Oroz Arizcuren 1979a.
- Beltrán Villagrasa 1948.
- Fletcher Valls & Silgo Gauche 1995, 274.
- Ballester Tormo 1930, 17.
- Lazaro Mengod et al. 1981, 173‑174.
- Fletcher Valls & Silgo Gauche 1995, 274.
- Lazaro Mengod et al. 1981, 174 ; Fletcher Valls & Silgo Gauche 1995, 274.
- Lucas Pellicer 1990.
- Lucas Pellicer 1990, 64.
- Grau Mira & Moratalla Jávega 2003.
- Grau Mira & Moratalla Jávega 2003, 27‑28.
- Grau Mira & Moratalla Jávega 2003, 40‑42.
- Grau Mira & Moratalla Jávega 2003, 42‑43.
- Grau Mira & Moratalla Jávega 2003, 43‑44.
- Ballester Tormo 1930, 12, 21‑22.
- Ballester Tormo 1930, 16‑23.
- Fletcher Valls & Silgo Gauche 1995, tableau 7.
- Grau Mira & Moratalla Jávega 2003, tableaux 3-5.
- Grau Mira & Moratalla Jávega 2003, 50.
- Poigt 2015a.
- Cuadrado Díaz 1964.
- Poigt 2015a, 144.
- Grau Mira & Moratalla Jávega 2003, 50.
- Delanaye & Poigt 2020.
- García-Bellido 2003.
- Maluquer de Motes & Pallarés Comas 1981.
- García-Bellido 2003, 153‑155.
- Celestino Pérez, éd. 2003, 109 ; García-Bellido 2003, 150.
- García-Bellido 2003, 148‑155.
- García-Bellido 2003, 140‑145.
- García-Bellido 2003, 142‑144.
- García-Bellido 2003, 146.
- Elayi & Elayi 1997, 319‑320.
- Maluquer de Motes 1983, 81‑83 ; García-Bellido 2003, 131.
- García-Bellido 2003, 141.
- Grau Mira & Moratalla Jávega 2003, 27.
- Llanos 1976 ; Llanos 1983 ; Galilea Martínez & Llanos Ortiz de Landaluze 2002 ; Llanos 2005.
- Labeaga Mendiola 1999.
- Peñalver Iribarren 2008 ; Peñalver & San Jose 2011 ; San José et al. 2015.
- Galilea Martínez 2004.
- Galilea Martínez 2004, 244‑245.
- Poigt 2015a.
- Galilea Martínez 2004, 214.
- Galilea Martínez 2004, 242.
- Vilaça 2003 ; Vilaça 2011.
- Vilaça 2011, 155.
- Cuadrado Díaz 1964.
- Pulak 1996 ; Pulak 2000.
- Vilaça 2011, 157.
- Idem.
- Vilaça 2011, 155.
- Vilaça 2011, 159.
- Idem.
- Vilaça 2011, 160.
- Antunes 2017.
- Antunes 2017, fig. 3.
- Antunes 2017, 916.
- Ruiz-Gálvez Priego 2008, 28.
- Testart 2004, 9.
- Schmandt-Besserat 1992 ; Schmandt-Besserat 1996, chap. “A turning point in communication and data storage” ; Ruiz-Gálvez Priego 2008, 28.
- Ruiz-Gálvez Priego 2000, 277 ; Ruiz-Gálvez Priego 2008, 28.
- Sherrat 2003, 229.
- Schmandt-Besserat 1992 ; Schmandt-Besserat 1996.
- Rahmstorf 2010, 99‑100.
- Salzmann 1950, 80.
- Le plus grand morphème numéral de la langue française est “centilliard” et est égal à 10603.
- Salzmann 1950, 81.
- Saxe 1981, 81.
- Salzmann 1950, 82.
- Salzmann 1950, 83.
- Saxe 1981, 307.
- De Vries 1994, 564.
- Salzmann 1950, 78.
- Grube 2007, 131.
- Ascalone & Peyronel 2006, 478.
- Sur l’utilisation du système sexagesimal en Mésopotamie, voir notamment : Proust 2010a ; Proust 2016.
- Hagège 2009, Comptages.
- Testart 2004, 10.
- Idem.
- Attention au quiproquo.
- Page internet du gouvernement français consacré aux obligations en matière de poids et mesures : [en ligne] https://www.economie.gouv.fr/dgccrf/publications/juridiques/panorama-des-textes/Poids-et-mesures [consulté le 21 déc. 2021].
- Testart 2004, 11.
- Garnier et al., éd. 1989, 271‑284.
- Bien que parler d’un “système simple” relève de l’oxymore, cette formule parait ici décrire convenablement la situation au regard de la complexité que peuvent prendre certains systèmes numéraux ou métrologiques.
- Turnbull et al. 2006 ; Crappier 2016, 24‑26.
- Crappier 2016, 24‑26.
- Zheng 2004, 353.
- Buchsenschutz 2007, 143‑144 ; Gorgues 2010, 72-73 ; 406‑408 ; Gruel 2012, 142 ; Garcia 2012, 111.
- Poigt & Ruiz Darasse 2020.
- Poigt & Ruiz Darasse 2020.
- Newton 1759 ; Paty 1999.
- Sellato 2004, 245.
- Crappier 2016, 22.
- Le Roux 2004, 142‑144.
- Voir notamment Beltrán Villagrasa 1948, qui restitue entre autres une unité de 8,28809 g.
- Académie des inscriptions et belles-lettres (France) 1680, 275.
- Il s’agit bien là du poids en tant que force et non de la masse.
- Tarpini et al. 2001, 180.
- Garnier et al., éd. 1989, 102 note 2 ; Tarpini et al. 2001, 180‑188.
- Person 1836, 191.
- Sperber 1988a, 158.
- Person 1836, 131 ; Sonnet 1843, 238.
- Person 1836, 131 ; Sperber 1988a, 160.
- Sperber 1988a ; Sperber 1991.
- Hällström 1842 ; Arne 1918 ; Sperber 1988a, 159.
- Sperber 1988a, 160.
- Michailidou 2005, 17.
- Macdonald 2004, 331.
- Christensen 1993, 57.
- Macdonald 2004, 323.
- Pare 1999.
- Il est important de noter que dans le cas d’une contrefaçon, tous les procédés exposés ci-après sont similaires à la différence près que la “masse voulue” ou la “masse idéelle” est volontairement différente de l’étalon de référence théorique.
- Marquet & Marquet 1970, 40.
- Celestino Pérez, éd. 2003, 148.
- Pulak 1996, 318.
- Crappier 2016, 24.
- Van Driessche 2009, 55-57.
- Allen 2017, 4-26.
- Voir par exemple Robbiola 1990 ; Galtier et al. 2015, 53.
- David 2001, 22.
- David 2001, 23.
- Robbiola 1990, 41 ; David 2001, 25.
- Robbiola 1990, 42 et tableau II.2.
- David 2001, 25.
- Elayi & Elayi 1997, 288.
- Galtier et al. 2015, 53.
- Petruso 1992, 9 ; Sperber 1993, 613 ; Pulak 1996, 15, 20.
- Pakkanen 2011.
- Pulak 1996, 319.
- Idem.
- Cunliffe 1984a, 412.
- Idem.
- Poigt 2015b.
- Il est à noter que ce diamètre théorique a toutefois été vérifié à l’aide d’un pied-à-coulisse, confirmant la mesure.
- Sørensen & Rahmstorf 2016, fig. 10.
- Cunliffe 1984a ; Cunliffe & Poole 1991a.
- Pulak 1996.
- Pour une application de ces processus voir : Delanaye & Poigt 2020.
- Nickerson 1998.
- Powell 1979, 74-75 ; Pulak 1996, 40.
- Petruso 1992, 34.
- Petruso 1992, 78.
- Petrie 1926, 1-2.
- García-Bellido 2003, 146.
- Vilaça 2011, 148.
- Roscio et al. 2011, 181.
- Muller 2007a, 30-42.
- Llanos 1983, 122.
- Poigt 2013, 76-78.
- Poigt 2015a.
- Rien ne permet en effet d’assurer que lot de poids de balance en usage comporte un poids correspondant à l’unité du système métrologique en vigueur.
- Rahmstorf 2006, 10.
- Poigt 2015a.
- Poigt 2015a, 143-144.
- Kendall 1974.
- Thom 1955 ; Broadbent 1955 ; Broadbent 1956.
- Kendall 1974, 231.
- Broadbent 1955 ; Broadbent 1956.
- Kendall 1974, 239.
- Idem.
- Opération réalisée sur le logiciel MS Excel.
- Voir notamment : Petruso 1992 ; Pulak 1996 ; Pakkanen 2002 ; Rahmstorf 2006 ; Rahmstorf 2010 ; Pakkanen 2011.
- Petruso 1992, 74-75.
- Idem.
- Voir par exemple : García-Bellido 2011 ; Callegarin & Hiriart 2013 ; Milcent 2017.
- En statistiques, un échantillon est généralement considéré comme représentatif lorsqu’il contient un minimum de trente individus.
- https://tie.hypotheses.org/outils/les-outils-danalyse-metrologique/the-metrological-tool-box.